Graniastosłup prawidłowy n-kątny ma o 55 więcej przekątnych niż krawędzi - znajd wacuś: Graniastosłup prawidłowy n−kątny ma o 55 więcej przekątnych niż krawędzi − znajdź n.

ines: Graniastosłup ma n*(n−3) przekątnych. ( Z każdego wierzchołka wychodzą przakątne do wszystkich wierzchołków przy drugiej podstawie z wyjątkiem tego bezpośrednio pod danym wierzchołkiem i dwóch sąsiednich, bo wtedy zawierałyby się w ścianach). Krawędzi jest 3n. Zapisujesz równanie: n(n−3)+55=3n i rozwiązujesz.

5-latek: Gdzies widziale wzory na ilosc krawedzi scien przekatnych w ostroslupie i graniastoslupie Nawet tu na forum kiedys ktos podawal

wacuś: Dzieki za pomoc

pigor: ... , 2d_n= 2* ¹₂n(n−3)=n(n−3) − liczba przekątnych graniastosłupa, czyli podwojona liczba przekątnych jego podstawy (dlaczego proste)...

5-latek: Czesc pigor Chciales proste masz dwie

pigor: ... cześć ; cieszę się, ale dlaczego równoległe przecież do ... tanga trzeba dwojga (tu dwie) oj, tylko ... bez brudnych myśli) ; pozdrawiam . ...

wacuś: uzasadnienie wzoru: http://brasil.cel.agh.edu.pl/~09utbaranski/?x=podstawy&y=wielokat

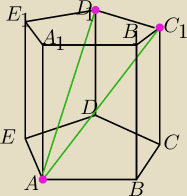
Lidka: Wacuś to co podałeś w linku dotyczy liczby przekątnych wielokąta. W zadaniu chodzi o takie przekątne, jak AD₁,AC₁. n=5 Z jednego wierzchołka mozna poprowadzić (5−3)=2 przekątne Wszystkich będzie 5*2=10 Do Twojego zadania należy ułożyć równanie : n*(n−3)=3n+55

wacuś: Lidka: tak, masz pełną rację, użyłem zbyt dużego skrótu myślowego, chodziło mi o uzasadnienie wyjściowe. Naturalnie w zadaniu należy użyć wzoru dotyczącego graniastosłupa, a nie wielokąta jak w linku

Lidka: