Funkcje cyklometryczne dobrelolo: Potrzebuje łopatologicznie rozpisane

	π
arctg(2x)<
	4

PW: Co to znaczy "rozpisane"? Chcesz rozwiązać nierówność?

	π
Wskazówka: co to znaczy, że		= arctg(u)?
	4

dobrelolo: tak chcę rozwiązać tą nierówność,

	pi
wiem, że arctg1=		bo to wie każdy
	4

	1
ale kolejne pytanie: czemu w arcsin(x)>1/2 jest odp. : sin		< x ≤ 1 a nie
	2

	π
np.		< x ≤ 1 ?
	2

Bo http://www.wolframalpha.com/input/?i=arcsin%28x%29%3E1%2F2 ?

	−π
Więc w tym arctg, zamiast mojego		< x <1 jaka powinna być odpowiedź?
	2

PW: No i nie wiem − pierwsze było tak łatwe, że niepotrzebnie pytałeś? Albo pytasz o jedno, albo o drugie. Nie ma takiej argumentacji "bo wolfram to ..."

dobrelolo: ale to pi/2 jest dobrze? czy to sin1/2? czy jest to dokładnie to samo? Mój mózg przeżywa właśnie niż funkcjonalny jak Polska po drugiej wojnie światowej. Proszę o ratunek Proszę o wersję dla osoby z nie pracującym mózgiem. Dziękuję.

dobrelolo: Nic się nie znalazło ?

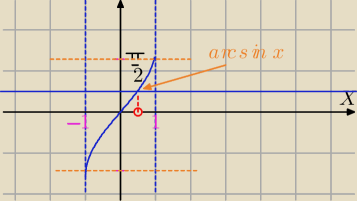Mila: y=arcsin(x) funkcja rosnąca dla x∊<−1,1>

	π		π
y=sin(x) funkcja rosnąca w przedziale <−		,		>
	2		2

	1
arcsin(x)>
	2

1		π
	<arcsin(x)≤		/obustronnie sinus
2		2

	1		π
sin		<sin(arcsin(x))≤sin(		)⇔
	2		2

	1
sin(		)<x≤1
	2

Mila:

	π
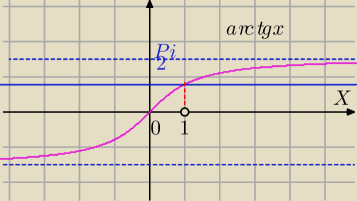
1) arctg(2x)<		⇔
	4

	π
arctg(2x)<		⇔
	4

	π
tg[arctg(2x)]<tg(		)⇔
	4

2x<1

	1
x<
	2