matematykaszkolna.pl
całka Matstud: Obliczyć objętość ograniczonych podanymi powierzchniami: x2+y2+z2−2z=0
 2π 
mi wychodzi
 3 
 π 
współrzędne sferyczne gdzie r∊(0,1) α∊(0,2π) β∊(0,
)
 2 
 4π 
w odpowiedzi
ktoś wie dlaczego?
 3 
2 paź 19:28
Matstud: pomocy
2 paź 20:04
Matstud: ?
2 paź 21:04
raz dwa trzy56: ja musze pomyśleć bo to trudne zadanie
2 paź 21:09
raz dwa trzy56:
2 paź 21:10
Kacper: x2+y2+(z−1)2=1 Kula o promieniu 1.
 4π 
V=
 3 
2 paź 21:12
Matstud: ale jak to wyszło?
2 paź 21:17
Kacper: Znasz wzór na objętość kuli? Nie ma sensu liczyć tego za pomocą całki.
2 paź 21:18
Matstud: ale właśnie musze użyć całek
2 paź 21:19
Kacper: To ja bym liczył z całki potrójnej, ale nie dziś, bo mam sporo pracy jeszcze.
2 paź 21:24
Matstud:
3 paź 21:17
Matstud:
 π π 
widze swój już błąd mianowicie β∊(−
,
) ale dlaczego tak jest
 2 2 
3 paź 21:21
Matstud:
3 paź 23:19
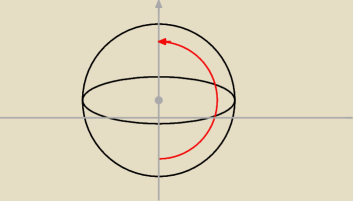
Godzio: rysunek Pewnie dlatego, trzeba sobie rysować takie rzeczy emotka
4 paź 00:39
Matstud: ale jest x2+y2+x2−2z=0 to coś zmienia?
4 paź 01:10
Matstud:
 −π π 
dlaczego dla x2+y2+z2−2z=0 β∊(
,
)
 2 2 
 π 
a na przykład dla x2+y2+z2≤z β∊(0,
)
 2 
5 paź 18:51