Równania kwadratowe z parametrem MysteriousCore: Wyznacz wszystkie wartości parametru m, dla których każde z dwóch różnych rozwiązań równania x²+x+m=0 jest większe od m. Wiem że pierwszy warunek powinien być Δ > 0, jednak jak będzie wyglądał drugi warunek i od razu prosiłbym z wyjaśnieniem

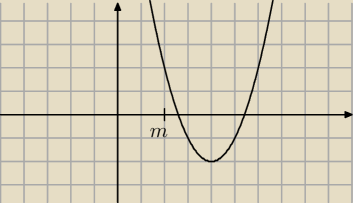
Kacper: Tak wygląda przykładowa parabole spełniająca warunki zadania. Postaraj się samemu/ej ustalić resztę warunków.

===: ... tak chyba nie do końca ...−

MysteriousCore: hmm to w drugim warunku ma być f(m) > 0 ?

Kacper: To nie wystarczy

===:

MysteriousCore: Do tej pory myślałem nad wykorzystaniem wzorów Viete'a i drugi przypadek ustaliłem, że będzie taki: 2) x₁−m>0, x₂−m> 0 (x₁−m)(x₂−m) > 0 3) (x₁−m)+(x₂−m) > 0 Czy dobrze myślę?

Kacper: Ok te dwa ostatnie warunki + Δ>0 jest w pełni poprawne. Rzadko kiedy używa się tej metody, ale jest ok

MysteriousCore: Na razie ciężko mi zrozumieć w inny sposób ale możliwe że dopiero są to moje początki i to jest powód, że jeszcze pewnych rzeczy nie widzę Wielkie dzięki za pomoc

Kacper: (tylko wtedy f(m)>0 jest niepotrzebny pamiętaj)

MysteriousCore: Tak wiem wiem

MysteriousCore: A jeszcze pytanie , bo mam jeszcze zadanie następne: Wyznacz wszystkie wartości parametru m, dla których każde z dwóch różnych rozwiązań równania x²−(2m−3)x+m=0 jest mniejsze od m. Czy warunki będą takie? 1) Δ > 0 2) (x₁−m)(x₂−m) > 0 3) (x₁−m)+(x₂−m) < 0

Kacper:

===: widzę to troszkę inaczej Sporo wiemy o tej paraboli. a>0 ...."uśmiechnięta" x_w=−1/2 y_w=m−1/4 m<0 1) Dwa różne pierwiastki Δ>0 czyli 1−4m>0 ⇒ m<1/4 2) f(m)>0 m²+2m>0 m(m+2)>0 m<−2 lub m>0 3) f(−m)>0 m²−m+m>0 m²>0 Ostatecznie m<−2

MysteriousCore: Właśnie się nie zgadza, w odpowiedziach mam podane m∊(0, 4−√7/2) ∪ (4+√7/2, 4) dzielone przez 2 dotyczy też 4

===: to pewnie źle zapisałeś wzór funkcji

MysteriousCore: Właśnie o dziwo wszystko się zgadza...

===: a jak może się zgadzać? x_w=−1.2 przy dodatnim m przynajmniej jeden pierwiastek musi być ujemny więc nie spełnia założenia że jest większy od m

===: miało być x_w=−1/2

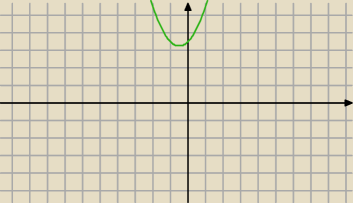
===: to jest f(x)=x²+x+3,5 widzisz tu pierwiastki?

===: ... i co ....sprawdziłeś? ... czy dałeś nie tylko nogę ...

MysteriousCore: O mnie mowa?

===: a o kim ?

Kacper: Prawidłowa odpowiedź w przykładzie z 18:54 to m∊(−∞,−2)

Kacper: Natomiast nie bardzo rozumiem np warunek m<0 u [P[===] Nie wiem skąd to się wzięło. Na pewno nie z tego zadania. Co oznacza warunek f(−m)>0 ?

MysteriousCore: Akurat tamto zadanie mi się zgodziło tylko chodzi że m∊(0, 4−√7/2) ∪ (4+√7/2, 4) to odpowiedz do tego drugiego

Kacper: To już trzeba liczyć Ja nie mam czasu.

MysteriousCore: Ale rozumiem, że te warunki nie są do końca poprawne? 1) Δ > 0 2) (x1−m)(x2−m) > 0 3) (x1−m)+(x2−m) < 0

Kacper: Dlaczego nie?

MysteriousCore: już tak mi zagmatwaliście że nie pogubiłem, w takim razie stosuję te co podałem powyżej

===: ... nie zauważyłem, że wprowadził tu drugie zadanie. Wszystko co pisałem to dotyczyło tego pierwszego. Czego Kacper nie rozumiesz? To wszystko z analizy danych. Skoro x_w=−1/2 a oba pierwiastki mają być większe od m ... to m<0 Jeśli tak to jeden jest dodatni a drugi ujemny a warunek f(m)>0 to już oczywista oczywistość