Twierdzenie Talesa Łukasz: Dane są odcinki długości odpowiednio x oraz y.. Skonstruuj taki odcinek długości a, że:

	x2 + y2
a) a=
	x + y

	x3
b) a=
	y2

Bardzo proszę o pomoc na jutro mam to zrobić a jestem zupełnie zielony w tym twierdzeniu Talesa

Kacper: Już wiesz gdzie szukać twierdzenie Talesa.

Łukasz: Dzięki Kaper za pomoc. Bardzo mi pomogłeś (sarkazm) −,−

Łukasz: jeżeli ktoś mógłby mi pomóc to proszę rozwiązanie przesłać na lukasz.r1@onet.pl

5-latek: A zamiast byc taki sarkastyczny to moze bys zajrzal do ksiazki albo poszukal w internecie ? Cos mi sie wydaje ze dostaniesz pewnie z 50 odpowiedzi na emala

Łukasz: Patrzyłem do książki nie ma podobnego przykładu a w internecie też nie znalazłem i przez to natrafiłem na to forum. Znam prawo Talesa (nawet zrobiłem podpunkt "b", ale "a" nie umiem.

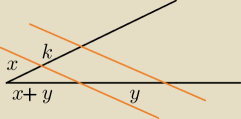
Jakub: Podpowiedzi:

	x2+y2		x2+2xy+y2−2xy		(x+y)2−2xy
a =		=		=		=
	x+y		x+y		x+y

	(x+y)2		2xy		xy
=		−		= x+y − 2 *
	x+y		x+y		x+y

	xy
k =
	x+y

Rysunek jest trochę niedokładny, bo odcinek y wyszedł mi dłuższy niż x+y. To do poprawienia.

	xy
Jednak idea, jak wyznaczyć k =		jest chyba jasna.
	x+y

Łukasz: @Jakub Jestem bardzo Tobie wdzięczny Jako jedyny mi pomogłeś. Dziękuję bardzo