am0 jerey: witajcie, mam problem z kilkoma równaniami z analizy matematycznej.

	π
cos(log9x4)−3sin(		+log3x)=cos(log√(3))
	2

tutaj kombinowałem w ten sposób: cos(log₉x⁴)−3(−cos(log₃x))=cos(log_√(3)1) cos(4log₉x⁴)+3cos(log₃x)=cos(log_√(3)1) sprowadziłem do logarytmu o podstawie √3

	1		1
cos(		log√3x)+3cos(		log√3x)=cos(log√31)
	4		2

i tu utknałem, zastanawiam się nad zastosowaniem wzorów na kąty połówkowe jednak nie wiem czy cokolwiek to da. kolejną równość próbowałem analogicznie lecz dalej nie mogę jej rozwiązac.

	3
log4sin(2x)+log2cos(		π+x)=log1/4tan(x)
	2

i kolejne:

	1
91+ctg2(π−x)=		sin(2x−π/2)−4 w przedziale x∊(5,10)
	3

tutaj z kolei rownanie wykładnicze sprowadziłem do rownania liniowego: 2ctg²x+2=cos2x+4 i nie bardzo wiem jak rozwiązać rownanie trygonometryczne w przedziale (5,10) zadanka są tutaj http://prac.im.pwr.wroc.pl/~pietrasz/listy/am0.pdf

J:

	π		π
... do pierwszego: sin(		+log3x) = cos(		+log3x) .. i co to jest: cos(log√3) ?
	2		2

jerey: przepraszam tam powinno być cos(log_√31)

	π		π
sin(		+log3x)=cos(		+log3x) tego przejścia nie rozumiem?
	2		2

J: .... ⇔ cos(2log₃x) − 3cos(log₃x) = 1 (podstawienie: t = log₃x) ⇔ cos2t − 3cost = 1 ⇔ 2cos²t − 3cost − 2 =0 ( podstawienie: u = cost)

ZKS:

	π
sin[		+ log3(x)] = −cos[log3(x)]
	2

jerey: @ZKS to wiem, zastosowałem juz wzór redukcyjny

J:

	π
...sorry ... miało być: sin(		+ log3x) = cos(log3x)
	2

J: @ZKS ... nie łapię , sin(90+α) = cosα ... skąd minus ?

ZKS: Chochlik.

J: ...

jerey: ok, to juz poleci. dziekuje. a równanie wykładnicze w przedziale (2;5) ?

ZKS: Szukasz tych rozwiązać gdzie x ∊ (2 ; 5).

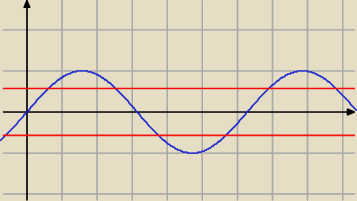
jerey: jak mam znaleźć te rozwiązania w x∊(2;5)? mam;

	√2		√2
sinx=		⋁−
	2		2

	π		5π
x1=		+2kπ x1=		+2kπ
	4		4

	3π		7π
x2=		+2kπ x2=		+2kπ
	4		4