monotoniczność john2: Kolejny kłopot z monotonicznością. Funkcja ma postać y = (x−1)³(2x+1)⁴. Wykres: http://www.wolframalpha.com/input/?i=plot+%28x-1%29^3%282x%2B1%29^4 1) Dziedzina x ∊ R 2) y' = (x−1)²(2x+1)³(14x−5) Dziedzina pochodnej: x ∊ R 3) y' = 0 (x−1)²(2x+1)³(14x−5) = 0

	1		5
(x−1)2(x+		)3(x−		) =0
	2		14

	1		5
x = 1 ∨ x = −		∨ x =
	2		14

4) y' > 0

	1		5
(x−1)2(x+		)3(x−		) > 0
	2		14

	1		5
x∊(−∞,−		)∪(		, 1)∪(1,∞) w tym przedziale funkcja rośnie (bez jedynki)
	2		14

5) y' < 0

	1		5
(x−1)2(x+		)3(x−		) < 0
	2		14

	1		5
x ∊ (−		,		) w tym przedziale funkcja maleje
	2		14

	1		5
Odpowiedź autora: funkcja rośnie dla x ∊(−∞,−		) ∪ (		, + ∞), (z jedynką)
	2		14

	1		5
maleje dla x ∊ (−		,		)
	2		14

Pytanie: czy obie wersje odpowiedzi są dopuszczalne? Z jedynką i bez jedynki?

Kacper: Oczywiście, że 1 ma być uwzględnione. Popatrz na przykład f(x)=x³ Badasz pochodną i wyrzucasz 0, ale przecież funkcja ta jest rosnąca w całej dziedzinie.

Kacper: Jeśli funkcja jest różniczkowalna w przedziale (a,b) oraz f'(x)≥0, to funkcja jest rosnąca w (a,b)

john2: Hmm. Bo tu jest napisane https://matematykaszkolna.pl/strona/381.html f'(x) > 0 i tak zawsze robiłem. Czyli najlepiej, jeśli chcę zbadać znak pochodnej, rozwiązać takie nierówności? f'(x)≥0 oraz f'(x) < 0

john2: Może zasada jest taka? Rozwiązuję: f'(x) > 0 i f'(x) < 0 tak jak zrobiłem. Jeśli natknę się na sytuację, że: Funkcja rośnie dla x ∊ (a,b) i dla x∊(b,c) (gdzie a < b < c). Jeśli b należy do dziedziny, to funkcja rośnie dla x∊(a,c). Analogicznie z malejącą funkcją. Co Wy na to?

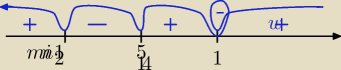
daras: n 1 jest punkt przegięcia ale funkcja nadal rośnie trzeba spr. znak y''

john2: Chyba za wysokie progi to jednak dla mnie. Dziękuję za odpowiedzi.

daras: Normalnie badasz znak pochodnej czyli rozwiązujesz nieróność:

	1		5
112(x − 1)2(x +		)3(x −		) > 0
	2		14

lub metodą pętelkową, postaram się wyraźniej namalować widać, że przechodząc przez x = 1 pochodna nie zmienia znaku tylko ma miejsce zerowe (punkt przegięcia) z wypukłej zmienia sie we wklęsła (albo odwrotnie−zależnie od definicji) ale cały

	1		5
czas rośnie więc ogólnie funkcja jest rosnąca dla x ∊(−∞; −		) ∪ (		; +∞).
	2		14

john2: Chyba rozumiem. Dziękuję daras.