Parabole sabuk: Pekształc parabole o rownaniu y=f(x) przez symetrie względem prostej l a nastepnie napisz rownanie otrzymanej paraboli f(x)=2(x−2)²−4 L:x=−1 f(x)=2(x−2)² −4 l:y=2 f(x)=−2(x+1)²+3 l:x=−3

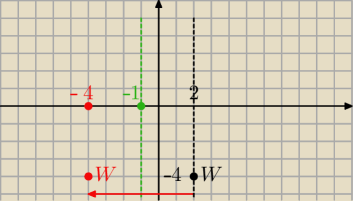
J: a) parabola posiada oś symetrii .... tutaj x = 2 .... aby uzyskać parabolę w symetri względem prostej l, wystarczy przesunąć ją o wektor v = [−6,0] .... popatrz na rysunek przesuniemy wierzchołek paraboli W(2,−4) o wektor v = [−6,0] .... po przesunięciu wierzchołek ma współrzędne: W'(−4,−4) zatem równanie paraboli po przekształceniu: f(x) = 2(x +4) − 4