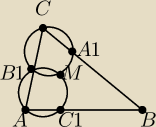
Wykaż, że punkt M należy do okręgu Pb: Na boku AB trójkąta ABC wybieramy dowolnie punkt C₁. Podobnie na boku BC wybieramy punkt A₁, a na boku AC wybieramy punkt B₁. Na trójkątach A₁B₁C i AB₁C₁ opisano okręgi, które przecięły się w punktach B₁ i M (zobacz rysunek). Wykaż, że do okręgu opisanego na trójkącie A₁BC₁ należy punkt M.

Andrzej: rozwiązywałem to zadanie na forum, chyba z rok temu: warunek opisania okręgu na czworokącie: sumy miar przeciwległych kątów mają po 180 stopni szkic rozwiązania: oznaczamy kąty trójkąta odpowiednio α β γ kąt B₁MC₁ ma 180−α kąt B₁MA₁ ma 180−γ stąd obliczamy kąt A₁MC₁ i pokazujemy że jest równy 180−β, co wystarczy, żeby na BA₁MC₁ opisać okrąg

Eta: To twierdzenie Miguela