s force:

	1
niech f(x)=log		x3+3x
	2

Uzasadnij ,że jeśli 0<a<b to f(a)<f(b)

force: poprawka ...to f(a)>f(b)

force: ?

Tadeusz: zapisz porządnie ten logarytm

Tadeusz: to jest f(x)=log_1/2(x³+3x) czy log_1/2x³+3x

force: f(x)=log_1/2(x²+3x)

Tadeusz: pod logarytmem jest x³+3x czy x²+3x

force: x³+3x

Tadeusz: 1) funkcja logarytmiczna dla podstawy większej od 0 a mniejszej od 1 jest ? 2) Wyrażenie logarytmowane w określonym przedziale rośnie (musisz to dowieść) 3) Wnioski

force: 1. funkcja malejąca 2.nie rozumiem w jakim przediale ma to wyrażenir rosnąć

force: nie rozumiem

Tadeusz: 0<a<b oczywiście

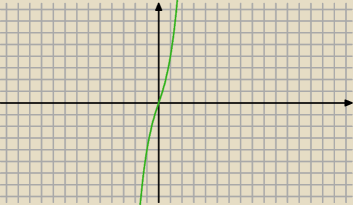
Tadeusz: ... to że x³+3x>0 ... to wynika z założenia dla logarytmu Interesuje nas jednak czy wyrażenie to dla x>0 rośnie czy maleje f(x)=x³+3x ⇒ f(x)=x(x²+3) Widzisz, że rośnie ...czyli dla b>a b³+3b>a³+3a i dalej chyba już jasne −

force: ooo no teraz to widze dzięki