monotonicznosc, pochodne
pawel95: wyznacz przedzialy monotonicznosci funkcji sinx + cosx, 0≤x≤2π
1 paź 13:35
5-latek: A to nie jest funkcja
1 paź 13:36
pawel95: f(x) = sin x + cos x
1 paź 13:43
Tadeusz:
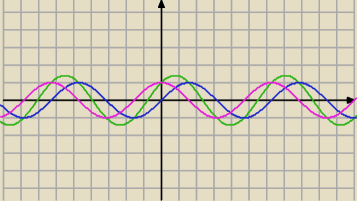
1 paź 15:06
PW:
| | π | | π | | π | |
f(x) = cosx + sinx = sin( |
| +x) + sinx = 2sin( |
| +x)·cos |
| = |
| | 2 | | 4 | | 4 | |
| | π | | √2 | | π | |
2sin(x+ |
| )· |
| = √2sin(x+ |
| ) |
| | 4 | | 2 | | 4 | |
Znacznie łatwiej różniczkować i przyrównywać pochodną do zera.
1 paź 15:15
J:
.... a po co przyrównywać do zera ? ...

1 paź 15:18
Tadeusz: jeśli zna pochodne ... to zbada znak −

1 paź 15:28
PW: No a jak piszesz f '(x) > 0 to nie przyrównujesz do zera? Staropolszczyzny mi się zachciało, że
zacytuję klasyka.
1 paź 15:31
J:
..znak − tak , a zero w jakim celu w tym zadaniu ? ...

1 paź 15:31
PW: A pomyśl o funkcji h(x) = x3. Co ustalisz, jeżeli tylko rozwiążesz nierówność
h'(x) > 0 ?
1 paź 15:45
J:
.. a kto powiedział,że rozwiązuje tylko nierówność h'(x) > 0 ? ...
1 paź 15:53
PW: Nawet gdy będziesz chciał rozwiązać nierówność h'(x) < 0, to efekt będzie żaden − nie ma
takich x.
Jeszcze raz pytam − co ustalisz, gdy stwierdzisz, że h ma znak dodatni dla x≠0?
Przeczytaj jeszcze raz co napisałem o 15:15.
1 paź 15:58
Tadeusz:
PW jak zwykle przy swoim ... tyle, że z samego przyrównania do 0 ... NIC NIE WYNIKA
(ekstremum ... punkt przegięcia ...

?)
1 paź 16:14
PW: Inne mamy poczucie językowe. Tego o 15:31 nie czytałeś?
Dla mnie, i nie jestem w tym odosobniony, przyrównanie liczby do zera to odpowiedź na pytanie:
− Jest ta liczba zerem, czy też jest od zera większa, czy może mniejsza?
A do zbadania monotoniczności w całej dziedzinie nie wystarcza ustalenie gdzie f '(x) > 0
i gdzie f '(x) < 0, to elementarz.
1 paź 16:36




 ?)
?)