parametr-nierówność kwadratowa mic: Dana jest nierówność kwadratowa z parametrem m: x² +8x −7 +m < 0 a) wyznacz wszystkie wartości parametru m, dla których przedział (3;4) zawiera się w zbiorze rozwiązań tej nierówności. b) uzasadnij, że jeżeli dla pewnej wartości parametru m nierówność ta ma rozwiązanie w przedziale (3;4) to ma ona w tym przedziale nieskończenie wiele rozwiązań.

Tadeusz: a) Δ>0 ⋀ f(4)<0

Godzio: a) f(3) chyba też musi być ujemne?

mic: w a) będzie tak myślę: Δ>0 ⋀ f(3)<0 ⋀ f(4)<0 tylko nie wiem jak w b)

Tadeusz: b)wierzchołek ma dla x_w=−4 ... więc to oczywiste

Tadeusz: ... to chyba oczywiste Godzio skoro x_w=−4

Godzio: No tak, spojrzałem na to schematycznie

Tadeusz: −

mic: b) Δ=23−m wtedy wierzchołek to W(−4 ; (m−23)/4) i co wtedy?

Tadeusz: ... a ktoś Cię pyta o y−kową współrzędną wierzchołka?

Tadeusz: a Δ=64−4(n−7)=64−4n+28=92−4n

mic: jak mam to uzasadnić w b) x_w=−4 to wiem i co wtedy bo nie rozumiem

Tadeusz: najlepiej narysuj −

mic: to wtedy f(−12)<0 i f(4)<0 i Δ=23−m gdzie Δ>0 jest wtedy gdy m∊(−∞;23) i co

Tadeusz: ... chyba sam nie wiesz co wypisujesz −

mic: to jak mam sobie narysować żebym to zrozumiał ?

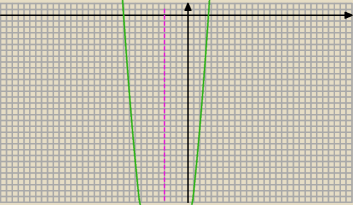
Tadeusz: Jeśli jeden pierwiastek zawiera siw przedziale (3,4) np. x₁=3,5 to drugi jest równo oddalony od osi symetrii Widzisz, że między 3 a x₁ jest nieskończenie wiele punktów

mic: ok dzieki teraz rozumiem

Tadeusz: −