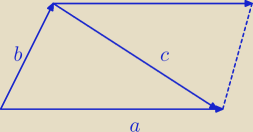
Wektor Piotr 10: Dlaczego c^→ = b^→ − a^→ ?

kochanus_niepospolitus: jak dla mnie to c^→ = a^→ − b^→

Piotr 10: b^→+c^→ = a^→ c^→ = a^→ − b^→ wg mnie też,

J: .... c^→ = a^→ − b^→ ..

Piotr 10: thx

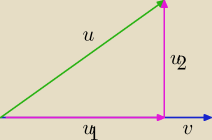
Piotr 10: Rzut prostokątny wektora u^→ na wektor v^→ Tw. ∀u^←≠0^→ , v^→≠0^→ ∃ u₁^→, u₂^→ takie, że u^→ = u₁^→+u₂^→ oraz u₁^→ II v^→ i u₂^→ ⊥v^→ Mam teraz przedstawić u₁^→ za pomocą u^→ i v^→ Pomoże ktoś ?

J:

	u→ O v→
u1→ =		*v→
	I v→I2

Piotr 10: Jak do tego doszedłeś ?

Piotr 10: ALbo sam spróbuje, widzę, że trzea iloczyn skalarny wykorzystać

Piotr 10: Możesz pokazać jednak ?

Piotr 10: Mam pytanie jeśli mam u^→ ◯ v^→ = u₁^→ ◯ v^→ To mogę podzielić obustronnie przez v^→ i wtedy

	u→ ◯ v→
u1→ =
	v→

5-latek: W tym CI nie pomoge bo nie pamietam Natomiast wczoraj pytales o rownoleglosc wektorow czyli α a+βb=0 (w tej rownosci 0 to wektor zerowy nie zas liczba 0 Masz to bardzo dobrze wytlumaczone w tej ksiazce http://allegro.pl/wektory-i-geometria-piegat-i4636139260.html

Piotr 10: Żebym miał tyle kasy. Wystarczy, że jutro kupuję dwie książki od jednej dziewczyny

J: .... a o b = IaI*IbI*cosα ... wyrażenie: IbI*cosα jeszt rzutem wektora b na wektor a ( b^→_a

Piotr 10: J mógłbyś coś więcej ?

J: (b^→_a) − oznacza rzut wektora b na wektor a ( i to jest wektor )

	a o b		a→
.... dalej ... b→a =		.... a ponieważ:		= 1 ... więc:
	IaI		IaI

	a o b		a→		a o b
b→a =		*		=		*a→
	IaI		IaI		IaI2

Piotr 10: Nie rozumiem, skąd ta pierwsza równość ?

Piotr 10: ?

J:

	a o b
popatrz na post 13:13 ... a o b = IaI*IbI*cosα = IaI*(b→a) ... stąd: b→a =
	IaI

Piotr 10: Dlaczego tak

I b→aI
	=cosα a nie tak ?
I bI

Piotr 10: ?

J: .... no tak, troche Ci zaciemniłem obraz...

	a o b
..... powinno być: a o b = IaI*IbI*cosα ⇔ IbI*cosα =		( skalar )
	IaI

ale, IbI*cosα*i^→ = (b^→_a) [ gdzie i^→ to wektor jednostkowy] .... to już jest wektor ( rzut wektora b na wektor a)

	a o b
...... i dalej : (b→a) =		*j→ ( wektor jednostkowy) .. i teraz za j→ mozemy
	IaI

	a→		a o b
podstawić:		otrzymując ostateczną zalezność: (b→a) =		*a→
	IaI		IaI2

Piotr 10: Ale nadal nie wiem czemu jest b^→_a = IbIcosα*i Skąd to się bierze

Piotr 10: Pomoże ktoś?

J: .... tutaj masz wyprowadzenie wzoru ( strona 26) ... http://www.math.uni.wroc.pl/~mgrec/2012/skrypt2.pdf

Piotr 10: DZIĘKI WIELKIE . W końcu to zrozumiałem . Dziękuję

Mila: 12:20 u₁^→=k*v^→, k∊R u₂^→=u^→−(u₁^→) u₂^→⊥v^→⇔u₂^→ov^→=0 (u^→−u₁^→) ov^→=0⇔ (u^→−k*v^→)ov^→=0⇔ u^→ov^→=k*|v|²=0

	u→ov→
k=
	|v|2

	u→ov→
u1→=		*v→
	|v|2

=============

Piotr 10: Dziękuję, już sobie poradziłem