wartość bezwzględna podpowiedź: Określ liczbę pierwiastków równania 2x² −5lxl −m =0 w zależności od wartości m

taliakart: myślę, że na początku trzeba z def. |x|, i trzeba rozpatrzyć dwa przypadki, w jednym bedzie identyczna postać równania a w drugim będzie 2x²+5x−m=0, poźniej dla kazdego przypadku liczysz delte i określasz zbiory rozwiązań

podpowiedź: proszę to pilne, tylko co z tą wartością zrobić ?

podpowiedź: dzięki tak też myślałem

taliakart: musisz rozbić na dwa przypadki, |x|=x dla x≥0 i |x|=−x dla x<0

Kacper: Najlepiej graficznie 2x²−5|x|=m Rysujesz to co po lewej stronie f(x)=2x²−5|x| i odczytujesz liczbę rozwiązań.

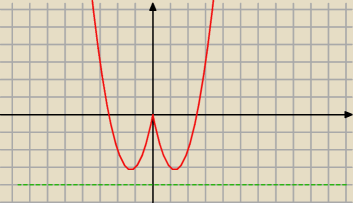
bezendu: 2x²−5|x|=m m∊(−∞,−3) brak rozwiązań m∊(3,0) cztery rozwiązania m∊{0} trzy rozwiązania m∊(0,∞)∪{3} dwa rozwiązania

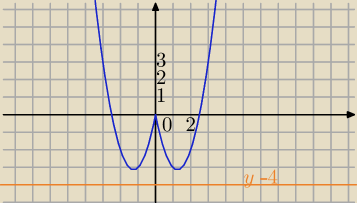
Mila: 2x² −5lxl =m f(x)=2x²−5|x| 1) wykres y=2x²−5x Miejsca zerowe: x(2x−5)=0

	5
x=0 lub x=
	2

	5
xw=
	4

	5		25		5		25
f(		)=2*		−5*		=−		wartość najmniesza f(x)
	4		16		4		8

2) wykres f(x)=2x²−5|x| Teraz odczytujesz dla jakich wartości m prosta y=m przecina wykres i w ilu punktach

	25
a)dla m<−		brak rozwiązań
	8

	−25
b) dla m=		dwa rozwiązania
	8

Dokończ sama?

podpowiedź: dzięki wielkie

Mila: