planimetria arli28: Na czworokącie ABCD, w którym AB= √3 −1, BC = 2, AC = √6, opisano okrąg. Wyznacz długości pozostałych boków czworokąta, wiedząc, że są one równe i oblicz promień okręgu.

Bogdan: Czworokąt ile ma boków?, długości ilu boków są podane?, długości ilu boków nie są podane?, długości których boków są równe?

arli28: AC to przekątna czworokąta.

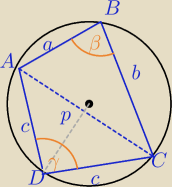
Mila: Powinnaś próbować sama, ponadto, jesli masz odpowiedź , to podaj. a=√3−1 b=2 p=√6 W ΔACB z tw. cosinusów: p²=a²+b²−2*a*b*cosβ (√6)²=(√3−1)²+2²−2*(√3−1)*2*cosβ 6=8−2√3−4*(√3−1)*cosβ −2+2√3=−4*(√3−1)*cosβ /:2 √3−1=−2*(√3−1) *cosβ

	1
cosβ=−		⇔β=120o
	2

γ=60 ^o bo γ+β=180^o ⇔ΔADC jest Δrównobocznym c=√6

	√6√3		√18		3√2
h=		=		=
	2		2		2

	2
R=		h
	3

dokończ

arli28: dzk. zrobiłam błąd w liczeniu z tw. cosinusów i nie wiedziałam co zrobić z wynikiem.

matylda: z jakiego zbioru jest to zadanie?

Miś Uszaty: Post ma 11 lat

matylda: ale z jakiego to zbioru