planimetria
arli28: Z punktu leżącego na okręgu poprowadzono dwie cięciwy o długościach 4cm i 8 cm. Oblicz promień
okręgu, jeżeli odległość między środkami cięciw wynosi 2 √7 cm.
29 wrz 22:49
Bogdan:
Wykonaj rysunek sam i poszukaj trójkątów podobnych
29 wrz 23:00
arli28: jakbym umiała, to bym zrobiła zadanie.
29 wrz 23:14
arli28: już wiem jak zrobić − wynik to 4 √21 / 3
29 wrz 23:38
arli28: trzeci bok to podwojona odległość między środkami.
wtedy liczymy jeden z kątów z tw. cos, a potem R z tw. sin.
29 wrz 23:40
Mila:
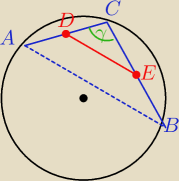
|AC|=4
|BC|=8
|DE|=2
√7
|AB|=4
√7, bo odcinek łączący środki boków Δ jest równy połowie boku trzeciego.
W ΔABC z tw. cosinusów:
(4
√7)
2=4
2+8
2−2*4*8*cosγ
16*7=16+64−64 cosγ
| | √3 | |
sin(120)=sin(180−60)=sin60= |
| |
| | 2 | |
Z tw. sinusów :
| AB| | |
| =2R podstaw i oblicz. |
| sinγ | |
29 wrz 23:41
 |AC|=4
|BC|=8
|DE|=2√7
|AB|=4√7, bo odcinek łączący środki boków Δ jest równy połowie boku trzeciego.
W ΔABC z tw. cosinusów:
(4√7)2=42+82−2*4*8*cosγ
16*7=16+64−64 cosγ
|AC|=4
|BC|=8
|DE|=2√7
|AB|=4√7, bo odcinek łączący środki boków Δ jest równy połowie boku trzeciego.
W ΔABC z tw. cosinusów:
(4√7)2=42+82−2*4*8*cosγ
16*7=16+64−64 cosγ