pomocy! ola: Określ liczbę rozwiązań równania m(4^x−2^x)=1−m w zależności od wartości parametru m. Bardzo proszę o pomoc.

ola: w odp. jest, że dla m>⁴₃ równanie nie ma rozwiązań. czy mógłby ktoś mi wytłumaczyć skąd to się bierze?

Tadeusz: ...dobrze to przepisałaś?

ola: tak, na pewno. wyszło mi, że równanie ma dwa rozwiązania, gdy m∊(1,2)∪(2,∞); jedno rozwiązanie, gdy m∊(0,1>∪{2}, brak rozwiązań dla m∊(−∞,0> gdzie robię błąd?

pigor: .., to może np. tak : m=0, to równanie sprzeczne (sprawdź 0=1), a więc niech m(4^x−2^x)= 1−m i m≠0 ⇒ 4^x−2*¹₂*2^x= ¹_m+1 /+¹₄ ⇔ ⇔ (2^x−¹₂)²= ¹_m−³₄, więc równanie to ma rozwiązania ⇔ ⇔ ¹_m−³₄ ≥0 /*4m² ⇒ 4m−3m² ≥0 ⇔ −3m(m−⁴₃) ≥0 /:(−3) ⇔ ⇔ m(m−⁴₃) ≤ 0 ⇔ 0< m ≤ ⁴₃, a więc { 0 rozwiązań , gdy 0≤ m v m >⁴₃ ⇔ m∊(−∞;0] U (⁴₃;+∞) , f(m)= { 1 rozwiązanie , gdy m= ⁴₃ , { 2 rozwiązania , gdy 0 < m < ⁴₃ ⇔ m∊(0;⁴₃) ...

pigor: ... kurde tam miało być { 0 rozwiązań , gdy m ≤ 0, ... ale już dalej jest dobrze , bo tak : (−∞;0] ... itd.

ola: dzięki, ale jeszcze się nie zgadza... ma być: gdy m∊(0,1>∪{⁴₃} − 1 rozwiązanie gdy m∊(1,⁴₃) − 2 rozwiązania...

pigor: ..., no to wybacz,nie chce mi się grzebać w tym i szukać błędu, ale może ktoś, albo sama poszukaj sobie m "deltą"

Godzio: Można też standardowo z podstawienie 2^x = t > 0. W nawiasach rozpisywałem na czym polega poszczególny przypadek, trochę więcej pisania niż u pigora mt² − mt − 1 + m = 0 Dla m = 0 mamy: −1 = 0 sprzeczność − brak rozwiązań Dla m ≠ 0

	4
Δ = m2 − 4m(m − 1) = − 3m2 + 4m = − 3m(m −		)
	3

	m − 1
t1t2 =
	m

t₁ + t₂ = 1 1^o Brak rozwiązań.

	4
a) m ≠ 0 i Δ < 0 ⇒ m ∊ (−∞, 0) U (		,∞) (delta ujemna − brak rozwiązań(
	3

b) m ≠ 0 Δ ≥ 0 i t₁t₂ > 0 i t₁ + t₂ < 0 (suma jest dodatnia, więc to odpada) (jest co najmniej jeden pierwiastek ujemny, ale t > 0 więc sprzeczność) 2^o Jedno rozwiązanie a) m ≠ 0 i Δ = 0 i t₁t₂ > 0 i t₁ + t₂ > 0

	4		m − 1
m =		i		> 0 − warunek jest spełniony
	3		m

(delta = 0 więc jeden pierwiastek podwójny, musi być dodatni) b) m ≠ 0 i Δ > 0 i t₁t₂ < 0

	4
m ≠ 0 i m ∊ (0,		) i m ∊(0,1) ⇒ m ∊ (0,1)
	3

(delta dodatnia, iloczyn ujemny, więc jeden pierwiastek jest ujemny, ale t > 0 − sprzeczność, jeden odpada) c) m ≠ 0 i Δ > 0 i t₁ = 0 i t₂ > 0 t₁ + t₂ > 0 i t₁t₂ = 0 ⇒ m = 1 (jeden pierwiastek równy 0 i znów sprzeczność z t > 0, drugi dodatni) 3^o Dwa rozwiązania m ≠ 0 i Δ > 0 i t₁t₂ > 0 i t₁ + t₂ > 0

	4		4
m ∊ (0,		) i m ∊ (−∞,0) U (1,∞) ⇒ m ∊ (1,		)
	3		3

(delta dodatnia i oba pierwiastki dodatnie) Podsumowując:

	4
0 rozwiązań dla m ∊ (−∞, 0> U (		,∞)
	3

	4
1 rozwiązanie dla m ∊ (0,1> U {		}
	3

	4
2 rozwiązania dla m ∊ (1,		)
	3

Tadeusz:

	1−m
4x−2x=
	m

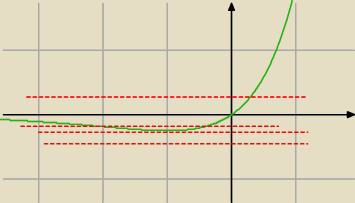
f(x)=4^x−2^x ma minimum równe −1/4 dla x=−1

ola: dziękuję, mi też w końcu wyszło dzięki za pomoc

pigor: ...no tak, nie dałem warunku na istnienie pierwiastków 2^|x| dodatnich.