określanie przedziałów
Adrian: Mam pytanko odnośnie przedziałów. Gdy mam postać nierówności
x(x+1)>0 ⇔ x∈(−∞,−1) ∪(0,+∞)
jak określić ten przedział z tej formy zdaniowej?
prosił bym o jakieś logiczne wytłumaczenie i rozpatrzenie np. przedziału x(x+1)<0 lub x(x−1)>0
29 wrz 21:27
Adrian: ta nierówność jest przedstawiona już w postaci sumy przedziałow ale skąd to się wzieło ?
29 wrz 21:33
5-latek:
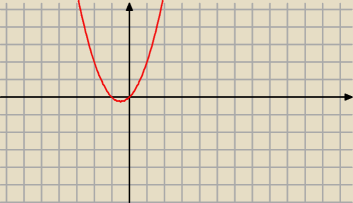
x(x+1)= x
2+x
To jest wykres funkcji y=x
2+x widzisz gdzie ta fucja jest >0 ?
29 wrz 21:36
PW: Iloczyn dwóch liczb jest dodatni wtedy i tylko wtedy, gdy
a) obie są dodatnie
lub
b) obie są ujemne,
to znaczy
(x> 0 i x+1 > 0) lub (x< 0 i x+1 < 0)
x > 0 lub x < −1
29 wrz 21:37
Mila:
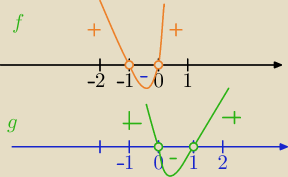
1)
f(x)=x*(x+1) to funkcja kwadratowa
Miejsca zerowe: x=0 oraz x=−1, wykresem jest parabola skierowana do góry.
a) x*(x+1)>0⇔x<−1 lub x>0
b) f(x)<0⇔(x*(x+1)<0⇔x∊(−1,0)
3) g(x)=x*(x−1) to funkcja kwadratowa
Miejsca zerowe:
x=0 oraz x=1
Parabola skierowana ramionami do góry:
x*(x−1)>0⇔x<0 lub x>1
x*(x−1)<0⇔x∊(0,1)
29 wrz 21:46
Adrian:
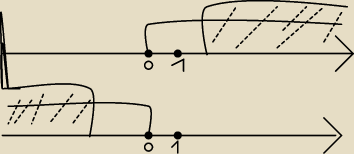
a gdy mamy x(−2+x)>0 to będzie (sam to robie) x(−2+x)>0⇔ [x>0 ⋀(−2+x)>0] ⋁ [x<0 ∧(−2+x)<0]
co źle tutaj zrobiłem

?
proszę nie patrzeć na zamalowane koła, tylko na same zbiory− i tak mialem trudnosci z
narysowaniem
29 wrz 21:52
Adrian: Dziękuje wszystkim trochę pomyślałem i od razu się rozjaśniło

jednak jakby ktoś życzył sobie mnie poprawić w ostatnim przykładzie było by miło

29 wrz 22:03
PW: x>0 ⋀(−2+x)>0, czyli x> 0 i x >2 narysowane dobrze.
x < 0 ∧(−2+x)<0, czyli x < 0 i x < 2 narysowane źle, bo pewnie zamiast napisać, zrobiłeś to w
pamięci (nie warto, to częsta przyczyna pomyłek).
29 wrz 22:24
 x(x+1)= x2+x
To jest wykres funkcji y=x2+x widzisz gdzie ta fucja jest >0 ?
x(x+1)= x2+x
To jest wykres funkcji y=x2+x widzisz gdzie ta fucja jest >0 ?
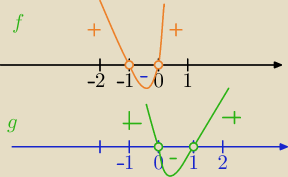 1)
f(x)=x*(x+1) to funkcja kwadratowa
Miejsca zerowe: x=0 oraz x=−1, wykresem jest parabola skierowana do góry.
a) x*(x+1)>0⇔x<−1 lub x>0
b) f(x)<0⇔(x*(x+1)<0⇔x∊(−1,0)
3) g(x)=x*(x−1) to funkcja kwadratowa
Miejsca zerowe:
x=0 oraz x=1
Parabola skierowana ramionami do góry:
x*(x−1)>0⇔x<0 lub x>1
x*(x−1)<0⇔x∊(0,1)
1)
f(x)=x*(x+1) to funkcja kwadratowa
Miejsca zerowe: x=0 oraz x=−1, wykresem jest parabola skierowana do góry.
a) x*(x+1)>0⇔x<−1 lub x>0
b) f(x)<0⇔(x*(x+1)<0⇔x∊(−1,0)
3) g(x)=x*(x−1) to funkcja kwadratowa
Miejsca zerowe:
x=0 oraz x=1
Parabola skierowana ramionami do góry:
x*(x−1)>0⇔x<0 lub x>1
x*(x−1)<0⇔x∊(0,1)
 a gdy mamy x(−2+x)>0 to będzie (sam to robie) x(−2+x)>0⇔ [x>0 ⋀(−2+x)>0] ⋁ [x<0 ∧(−2+x)<0]
co źle tutaj zrobiłem
a gdy mamy x(−2+x)>0 to będzie (sam to robie) x(−2+x)>0⇔ [x>0 ⋀(−2+x)>0] ⋁ [x<0 ∧(−2+x)<0]
co źle tutaj zrobiłem ?
proszę nie patrzeć na zamalowane koła, tylko na same zbiory− i tak mialem trudnosci z
narysowaniem
?
proszę nie patrzeć na zamalowane koła, tylko na same zbiory− i tak mialem trudnosci z
narysowaniem
 jednak jakby ktoś życzył sobie mnie poprawić w ostatnim przykładzie było by miło
jednak jakby ktoś życzył sobie mnie poprawić w ostatnim przykładzie było by miło 