OBLICZ KAT: Oblicz sumie wszystkich rozwiazan rownania : sinX= 0,7 , ktore naleza do przedziału <0;6pi>

Kacper: 0.7?

KAT: tak jest w zadaniu

KAT: podejrzalem wynik zadania i jest 15pi ale nie wiem jak to rozwiazac

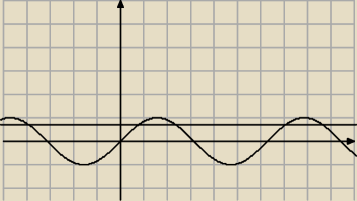
Kacper: To rysuj i odczytuj

KAT: nie ma jakiegos wzoru do tego zadania ? pomoz mi je rozwiazac jesli mozesz

Mila: sinx=0,7⇔ x=arcsin(0,7)+2kπ lub x=π−arcsin(0,7)+2kπ Oznaczmy x₁=arcsin(0,7) Sumujemy: x₁+( x₁+2π)+( x₁+4π)+ (π−x₁)+(π−x₁+2π)+(π−x₁+4π) ========================= =15π

Kacper: W liceum nie ma arcsinx

KAT: no mam rozszerzona matme ale nie wiem co to arcsinx , jakos inaczej sie to da zrobic ?

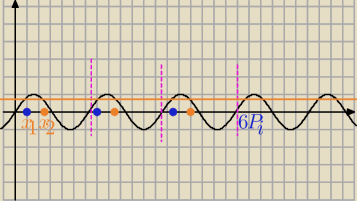
Mila: To nie ma znaczenia tutaj, oznacz rozwiązanie x₁ albo daj przybliżoną wartość z tablicy. sinx=0,7 x₁≈44⁰ Jeśli umiesz rozwiązać elementarne rozwiązanie to wypisz serie rozwiązań. x₁,x₁+2π,x₁+4, (π−x₁)+(π−x₁+2π)+(π−x₁+4π)

PW: Po prostu rozwiązania równania sinx = a dla a∊(0,1) na przedziale [0,π) są symetryczne względem prostej

	π
x =		,
	2

czyli spełniają zależność

	x1 + x2		π
(1)		=
	2		2

Na przedziale [π, 2π) rozwiązań nie ma. W następnym przedziale o długości 2π rozwiązania spełniają warunek

	x3 + x4		π
(2)		=		+ 2π,
	2		2

a na następnym

	x5 + x5		π
(3)		=		+ 4π,
	2		2

Na zadanym przedziale (0,6π) suma rozwiązań wynika z zsumowania (1), (2) i (3) − to jest to samo co napisała Mila.

PW: Poprawka

	x5+x6
(3)		= ...
	2

Mila: Jeśli dalej nie rozumiesz, to rozwiąż to zadanie dla równania :

	π
sin(x)=		i wypisz wszystkie rozwiązania w przedziale (0,6π), a następnie zsumuj.
	6

PW: O, na przykładzie dobrze jest raz chociaż zrobić, to się rozjaśnia, że wcale nie muszę znać tych rozwiązań dla obliczenia sumy.

Mila: Najwyraźniej zlekceważyła nasze wyjaśnienia.

PW: