Zadanko Jacek: Znaleźć prostą przechodzącą przez punkt (2,3) wiedząc, że jej odcinek zawarty miedzy prostymi 3x+4y−7=0 i 3x+4y+8=0 jest równy 3√2. Mógłby mi ktoś pomóc w zrobieniu tego zadania najprostszym sposobem

===:

pigor: ..., a studia, czy liceum ? , i albo czy może być wektorowo i z parametrycznymi równaniami prostych

Jacek: technikum wektorami możesz operować

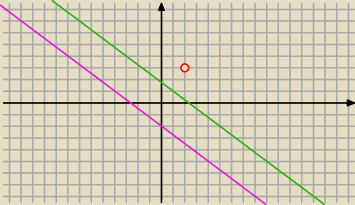
pigor: ..., no to jak na technikum np. tak : szukasz prostej y=mx+n przez punkt (2,3), więc 3=2m+n ⇒ n=3−2m i y=mx+3−2m, czyli (*) y=m(x−2)+3= prosta ta przecina dane 2 proste równoległe (ich współczynniki przy x, y są równe) w punktach (x,y) będących rozwiązaniem układów równań : ((**) y=mx−2m+3 i 3x+4y−7=0) v (y=mx−2m+3 i 3x+4y+8=0) ⇒ ⇒ 3x+4mx−8m+12−7=0 v 3x+4mx−8m+12+8=0 ⇔ ⇔ (3+4m)x=8m−5 v (3+4m)x=8m−20 ⇒

	8m−5		8m−20
⇒ x=		v x=		a stąd i z (**) wyznaczasz
	3+4m		3+4m

odpowiednie y−eki i masz punkty przecięcia z danymi prostymi: (x,y) :

	8m−5		9+m		8m−20		9−14m
A=(		,		v B=(		,		), a
	3+4m		3+4m		3+4m		3+4m

ponieważ masz daną odległość tych punktów |AB|=3√2 ⇒ AB²=18 ⇒ ⇒ (X_B−X_A)²+(y_B−y_A)²=18 ⇔ (twoja robota) ,,, ⇔

	15		15m
⇔ (		)2+ (		)2=18 ⇔ 152+152m2=18(3+4m)2 /:9 ⇔
	3+4m		3+4m

⇔ 25+25m²=2(9+24m+16m²) ⇔ 7m²+48m−7=0 i √Δ= 50 , więc m= ¹₁₄(−98)= =7 v m= ¹₁₄*2= ¹₇. o ciekawe, bo szukane proste są prostopadle, no to jeszcze dalej stąd i z (*) : y= −7(x−2)+3 v y= ¹₇(x−2)+3 ⇔ 7x+y−17=0 v x−7y+1=0 − − szukane proste w postaci ogólnej uffffffffffff . .. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− p.s. chyba nie kopnąłem się bo ładna końcówka

Jacek: Dziękuję za pomoc