Prędkość i funkcja kwadratowa. humbak: Wbrew pozorom jest to (raczej) zadanie z matematyki: Pewne ciało porusza się ruchem prostoliniowym zgodnie ze wzorem s(t)=6t²−0,5t³, gdzie s(t) oznacza drogę mierzoną w metrach, natomiast t czas mierzony w sekundach. W którym momencie t∊<0,12> prędkość ciała jest największa? Oblicz tę prędkość.

	s
Zrobiłem to tak: prędkość to, o ile się nie mylę,		, więc tu podzieliłem wzór na s przez
	t

	t2
t. Wyszło 6t −		. Jest to f. kw. której a<0, więc wierzchołek p=6 jest punktem o
	2

największej wartości. Czy jest to dobry sposób na rozwiązanie tego zadania (do tego momentu)?

J: ...to nie jest ruch jednostajny .... prędkość, to pochodna drogi po czasie ... v(t) = 12t −1,5t² ... i teraz szukaj maksimum w podanym przedziale..

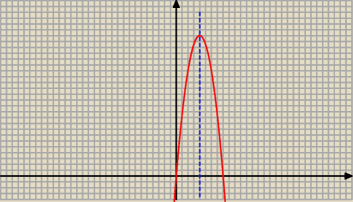
Janek191: v(t) = s '(t) = 12 t − 1,5 t² = t*(12 − 1,5 t) t = 0 lub t = 8

	0 + 8
p =		= 4
	2

v_max = v( p) = v(4) = 12*4 − 1,5*4² = 48 − 24 = 24 p = 4 s

	m
vmax = 24 [		]
	s

Jaszunex: Czy można prosić o wyjaśnienie, czemu v(t) jest równe pochodnej z s(t)?

Qulka: z definicji