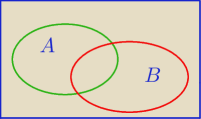
Prawdopodobieństwo różnicy zdarzeń Diament: Temat: Własności prawdopodobieństwa Niech A, B ⊂ Ω. Oblicz prawdopodobieństwo różnicy zdarzeń A \ B, jeśli: b) P(A∪B) = 9/10 i P(B) = 7/10 Znane mi wzory z tego tematu: 1. P(A\B) = P(A) − P(A∩B) 2. P(A∪B) = P(A) + P(B) − P(A∩B)

Lukas: P(A∪B)=P(A)+P(B)−P(A∩B) Pokaż przykład a) bo z tego nic nie policzysz...

Diament: a) P(A∩B) = 1/4 i P(A) = 3/8 Z tym, że ten przykład to akurat prościzna.. P(A\B) = P(A) − P(A∩B) = 3/8 − 1/4 = 1/8

Diament: Tak myśląc dłużej wywnioskowałem, że skoro (A−B) to jest A bez B, to to samo wyjdzie z (A∪B)−P(B). No i na tej podstawie: »» P(A−B)=P(A∪B)−P(B) «« Więc, P(A−B) = 9/10 − 7/10 = 2/10 = 1/5 A to by się zgadzało z odpowiedzią w książce. Nie wiem czy dobrze wywnioskowałem, ale odpowiedź się zgadza