Objętość graniastosłupa prawidłowego czworokątnego sowhat: Miara kąta zawartego między przekątnymi ścian bocznych graniastosłupa prawidłowego czworokątnego, wychodzącymi z tego samego wierzchołka, jest równa 60, a krawędź podstawy ma długość 4. Oblicz długość przekątnej tego graniastosłupa. Prosiłbym również o rysunek.

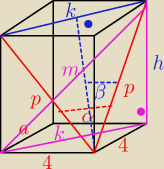
Janek191: α = 60^o a = 4 k = a√2 = 4 √2 β = 0,5*α = 30^o więc

0,5 k
	= sin β = sin 30o = 0,5
p

2√2
	= 0,5 ⇒ p = 4√2 ⇒ p2 = 32
p

Z tw. Pitagorasa mamy a² + h² = p² 4² + h² = 32 h² = 16 h = 4 ===== Długość przekątnej graniastosłupa m Mamy m² = k² + h² = ( 4√2)² + 16 = 32 + 16 = 48 = 16*3 więc m = √16*3 = 4√3 ================

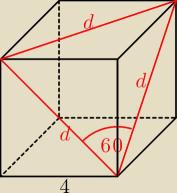
Bogdan: Co tu kombinować z obliczeniami. Jeśli miara podanego kąta jest równa 60^o, to trójkąt jest równoboczny, a graniastosłup jest sześcianem. Długość przekątnej tego sześcianu jest równa 4√3 i tyle.