Proszę o pomoc anonim: 1) Wyznacz wartość parametru m, dla których zbiór rozwiązań nierówności 3x+m−1<0 a)zawiera się w przedziale (−∞,1). 2)Wyznacz wartość parametru k, dla których zbiór rozwiązań nierówności 2x−3k≥5 a)zawiera się w przedziale (−5,+∞). Proszę o wyjaśnienie, kiedy w odpowiedzi będzie, że zbiór jest większy/mniejszy, a kiedy, że większy lub równy/mniejszy lub równy.

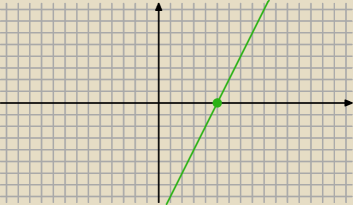
Tadeusz: 2) 2x−3k−5≥0 Rozpatrzmy f(x)=2x−3k−5 do wykresu tej funkcji należy punkt (−5, 0) zatem: 0=−10−3k−5 k=−5

pigor: ..., otóż z warunków zadania widzę to tak : 1) 3x+m−1< 0 i x<1 ⇒ 3x<1−m i x<1 ⇒ x< ¹₃(1−m) i x< 1 ⇒ ⇒ ¹₃(1−m) = 1 /*3 ⇔ 1−m=3 ⇔ 1−3= m ⇔ m= −2 ; −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2) 2x−3k ≥ 5 i x > −5 ⇒ 2x ≥ 3k+5 i x > −5 ⇒ x ≥ ¹₂(3k+5) i x > −5 ⇒ ⇒ [ x = ¹₂(3k+5) lub x > ¹₂(3k+5) ] i x > −5 ⇔ ⇔ ¹₂(3k+5) > −5 lub ¹₂(3k+5)= −5 ⇔ ¹₂(3k+5) ≥ −5 ⇔ ⇔ 3k+5 ≥ −10 ⇔ 3k ≥ −15 ⇔ k ≥ −5 ⇔ k∊ [−5;+∞) . ...