zadania - f.log. Blue: Mam kilka zadań, z którymi mam problemy : zad.9 a) i b) i d) zad10 c) Oto linki do treści zadań (będzie to bardziej przejrzyste, gdybym przepisywała to ² by się pewnie zlewały^^: http://i58.tinypic.com/es422a.jpg W tym zad.9 powiedzmy np. a) wiadomo, że log_ab <0, no bo to wynika z tego, w jakich przedziałach jest zawarte a i b. To, co jest do kwadratu, zawsze jest dodatnie. Zatem całe wyrażenie jest ujemne... Jednak czy takie słowne wytłumaczenie wystarczy? Wątpię. Jak to udowodnić, aby było dobrze udowodnione

razor: Słownie wystarczy wg mnie Można to "przetłumaczyć" na język matematyczny ale znaczenie będzie takie same

Blue: Serio? Słownie... A mógłbyś mi powiedzieć, jakbyś zrobił(może być słownie) podpunkt d), bo jakoś tak się nad tym zastanawiam...

razor: log²_ab+log_√ab ≥ −1 log²_ab+2log_ab+1 ≥ 0 (log_ab+1)² ≥ 0

Mila: 10 c, próbuj sama, poprawimy błędy D:... f(x)= wzór po przekształceniu.

Blue: f(x) = −1*log₂x

Mila: Nie. Najpierw dziedzina.

Blue: Razor dziękuję Ci

Blue: ahaa. D= R|{0}?

Blue: D= R\{0} *

Mila: Dobrze D, a w Twojej funkcji z 20:42?

Blue: no w mojej funkcji jest D=(0, ∞)

Mila: Zatem funkcje nie są równe.

	log2(x2)
f(x)=		−log2(x2)⇔
	2

	1
f(x)=		*2log2(|x|)−2log2(|x|)
	2

f(x)=−log₂(|x|) i rysuj , potem narysuję ja.

Blue: czyli będzie −log₂|x|, bo odbijamy

Blue: to już teraz wiem, Mila, jak to narysować Dziękuję

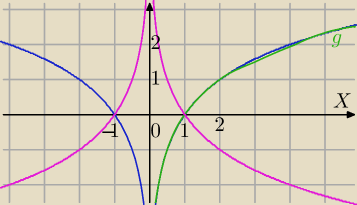
Mila: 1) g(x)=log₂(x) oczywiście dla x>0 (wykres z prawej) 2) S_OY ⇒y=log₂|x| 3) S_OX⇒f(x)=−log₂|x|