Przekątna prostopadłościanu...
Maciej: Przekątna prostopadłościanu ma długość 8 a miara kąta jaki ona tworzy ze ścianą boczną wynosi
30 stopni. Oblicz objętość i pole powierzchni całkowitej jeśli jego wysokość wynosi 2√7.
Pc=2Pp+Pś
Pc=2a2+4aH
a=?
V=Pp*H
V=a2*H
sin30=ad
12=a8
a=4
V= 32√7 cm3
Pc= 2*16+4*8√7=32+32√7
Pc=32(1+√7)
Czy tak można rozwiązać to zadanie? Czy jest poprawne?
25 wrz 21:13
J:
... a dlaczego Pp = a2 ?
25 wrz 21:15
Maciej: a nie możemy przyjąć, że w podstawie jest kwadrat?
25 wrz 21:16
J: Nie możemy ...bo nie ma o tym mowy w treści zadania..

jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
25 wrz 21:21
J: Nie możemy ...bo nie ma o tym mowy w treści zadania..

jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
25 wrz 21:21
Maciej: To tak krawędź podstawy wynosi 4
a przekątna ściany bocznej d12 = H2 + b2?
25 wrz 21:30
J:
Tak ... a = 4 .. i teraz: a2 + d2 = 8 ( gdzie d − przekątna ściany bocznej) d = √48
potem: b2 + H2 = (√48)2 b = 2√5
krawędzie podstawy: a = 4 , b =2√5 , H = 2√7 (pdana) Pc = 2(ab + aH + bH)
25 wrz 21:35
J:
Tak ... a = 4 .. i teraz: a2 + d2 = 8 ( gdzie d − przekątna ściany bocznej) d = √48
potem: b2 + H2 = (√48)2 b = 2√5
krawędzie podstawy: a = 4 , b =2√5 , H = 2√7 (pdana) Pc = 2(ab + aH + bH)
25 wrz 21:36
J: pierwsza linijka: ... oczywiście: a2 + d2 = 82
25 wrz 21:37
Eta:
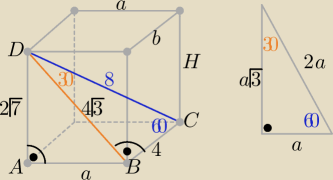
|BC|=4 , |BD|=4
√3 i H=|AD|=2
√7
|AB|=a=
√(4√3)2−(2√7)2=........
V= a*b*H=.... P
c= 2(ab+aH+bH)=.........
25 wrz 21:44
Maciej: Dziękuję bardzo

Wyszło mi tak: V= 16
√35 Pc= 16
√5+16
√7+8
√35
Czy dobrze?
25 wrz 21:47
Maciej: Mam jeszcze takie zadanie:
Podstawą graniastosłupa prostego jest romb, którego bok ma długość 5√3cm. Wiedząc, że
graniastosłup ma wysokość 8cm, a dłuższa przekątna graniastosłupa ma 17 cm, oblicz:
a) marę kata ostrego rombu
b) długość krótszej przekątnej graniastosłupa
25 wrz 21:54
Maciej: jest ktoś?
25 wrz 22:04
Eta:
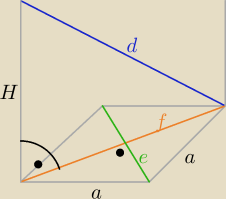
Z tw. Pitagorasa
f=
√d2−H2 ⇒ f=.........
w rombie: e
2+f
2=4a
2 ⇒ e=............= 5
√3 zatem a=e ⇒ α= 60
o
25 wrz 22:04
Maciej: Dziękuję f=15cm e=5√3 α=60 stopni
Długość krótszej podstawy d12=H2+a2, gdzie d12 − krótsza przekątna
d12=139
d1=√139cm
25 wrz 22:30
Maciej: Jeszcze chciałbym się zapytać

Czy da się zrobić takie zadanie?
Przekątna podstawy czworokątnego graniastosłupa prawidłowego wynosi 3
√2 i tworzy z przekątną
ściany kat o mierze 60 stopni. Oblicz objętość tego graniastosłupa.
25 wrz 22:31
Maciej: 
25 wrz 22:46
Eta:
Jasne,że da się

25 wrz 23:11
Eta:
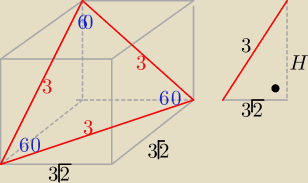
H=............. V=............
25 wrz 23:18
Eta:
Poprawiam chochlika
oczywiście,że zamiast d=3 ma być d= 6
bo d=3√2*√2=6
teraz sam dokończ...........
25 wrz 23:33
Maciej: a=3 chyba, nie?
bo d=a√2
3√2=a√2
a=3
H2=18−9
H=3
V=Pp*H=27
26 wrz 00:17
J:
Rysynek jest dobry, ale źle opisany ... przekątna podstawy ma długość d = 3√2 , zatem krawedź
podstawy ma długość: a = 3
Skoro przekątna podstawy jest taka sama jak przekątna ściany bocznej, to ten graniastosłup jest
sześcianem o krawedzi a, zatem objętość V = a3
26 wrz 10:07
Mateusz: Przekątna prostopadłościanu przedstawionego na rysunku tworzy z najdłuższa jego krawędzią kat
Alfa zatem
18 gru 13:17
 jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
 jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
jedna krawędż podstawy wylicz z funkcji sinus
następnie przekatna ciany bocznej(Pitagoras)
na końcu druga krawędż podstawy (Pitagoras) .... i po temacie
 |BC|=4 , |BD|=4√3 i H=|AD|=2√7
|AB|=a=√(4√3)2−(2√7)2=........
V= a*b*H=.... Pc= 2(ab+aH+bH)=.........
|BC|=4 , |BD|=4√3 i H=|AD|=2√7
|AB|=a=√(4√3)2−(2√7)2=........
V= a*b*H=.... Pc= 2(ab+aH+bH)=.........
 Wyszło mi tak: V= 16√35 Pc= 16√5+16√7+8√35
Czy dobrze?
Wyszło mi tak: V= 16√35 Pc= 16√5+16√7+8√35
Czy dobrze?
 Z tw. Pitagorasa
f=√d2−H2 ⇒ f=.........
w rombie: e2+f2=4a2 ⇒ e=............= 5√3 zatem a=e ⇒ α= 60o
Z tw. Pitagorasa
f=√d2−H2 ⇒ f=.........
w rombie: e2+f2=4a2 ⇒ e=............= 5√3 zatem a=e ⇒ α= 60o
 Czy da się zrobić takie zadanie?
Przekątna podstawy czworokątnego graniastosłupa prawidłowego wynosi 3√2 i tworzy z przekątną
ściany kat o mierze 60 stopni. Oblicz objętość tego graniastosłupa.
Czy da się zrobić takie zadanie?
Przekątna podstawy czworokątnego graniastosłupa prawidłowego wynosi 3√2 i tworzy z przekątną
ściany kat o mierze 60 stopni. Oblicz objętość tego graniastosłupa.


 H=............. V=............
H=............. V=............