kombinatoryka
zadanie:
1. Na ile wszystkich roznych sposobow mozna posadzic przy okraglym stole n osob? (Odp. (n−1)!)
Dwa sposoby rozsadzenia uważamy za jednakowe wtedy i tylko wtedy, gdy każda osoba ma tego
samego sąsiada z prawej strony i tego samego z lewej strony.
2. To samo zadanie ale, gdy dwa sposoby rozsadzenia uważamy za jednakowe wtedy i tylko wtedy,
| | (n−1)! | |
gdy każda osoba ma tych samych sasiadow. (Odp. |
| ) |
| | 2 | |
Nie rozumiem roznicy pomiedzy tymi zadaniami. Dla mnie wszyscy sasiedzi sa tacy sami.
Moglbym poprosic o wytlumaczenie tej roznicy dla konkretnego przypadku? (np. dla 4 osob).
Jezeli byloby to mozliwe to o rysunek tez bym poprosil.
25 wrz 13:29
MYSZ:
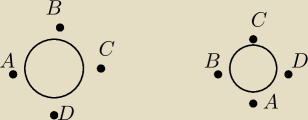
n osob na n miejsach rozstawisz na n! sposobow.
Ale jezeli kazda osoba wskoczy na miejsce obok, tak jak na rysunku − to bedzie caly czas taki
sam uklad ( A siedzi kolo B i D ) . Takich skokow moze wykonac n(u nas 4), wiec calosc trzeba
podzielic przez n.
| | n! | | n*(n−1)! | |
= |
| = |
| = (n−1)! |
| | n | | n | |
25 wrz 13:36
Mila:
1) W pierwszym przy obrocie masz taki sam układ siedzących osób.
2) W drugim zadaniu układ sąsiadów np. dla A:
BAD i DAB uznaje się za taki sam, to liczba ustawień:
25 wrz 17:14
zadanie: dziekuje
25 wrz 18:22
PW: Może jeszcze inaczej spojrzeć:
Każda permutacja
(x1, x2, x3, ..., xn)
ma "bliźniaczą" permutację
(xn, xn−1, ..., x3, x2, x1),
w której każdy element ma takie same sąsiednie. Dlatego − jeżeli "bliźniacze" permutacje uznamy
za równoważne w sensie usadzenia przy stole, to wynik z zadania a) trzeba podzielić przez 2.
W pierwszej wersji sąsiadami są xn i x1, a w "bliźniaczej" sąsiadami są x1 i xn (to tak dla
porządku − pokazujemy, że "permutacje się skleja" − początek z końcem − żeby uzyskać model
usadzania przy stole).
Geometrycznie − jeżeli już mamy rysunek elementów na okręgu − utworzenie "bliźniaczego"
usadzenia oznacza symetrię osiową o osi przebiegającej przez środek stołu między elementami
x1 a xn.
25 wrz 20:27
zadanie:
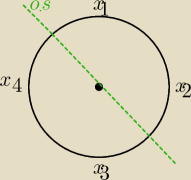
Dla 4 osob.
Permutacja (x
1, x
2, x
3, x
4).
,,Blizniacza permutacja'' (x
4, x
3, x
2, x
1)
26 wrz 01:58
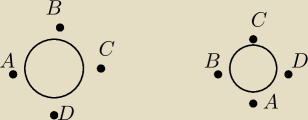 n osob na n miejsach rozstawisz na n! sposobow.
Ale jezeli kazda osoba wskoczy na miejsce obok, tak jak na rysunku − to bedzie caly czas taki
sam uklad ( A siedzi kolo B i D ) . Takich skokow moze wykonac n(u nas 4), wiec calosc trzeba
podzielic przez n.
n osob na n miejsach rozstawisz na n! sposobow.
Ale jezeli kazda osoba wskoczy na miejsce obok, tak jak na rysunku − to bedzie caly czas taki
sam uklad ( A siedzi kolo B i D ) . Takich skokow moze wykonac n(u nas 4), wiec calosc trzeba
podzielic przez n.
 Dla 4 osob.
Permutacja (x1, x2, x3, x4).
,,Blizniacza permutacja'' (x4, x3, x2, x1)
Dla 4 osob.
Permutacja (x1, x2, x3, x4).
,,Blizniacza permutacja'' (x4, x3, x2, x1)