planimetria
Pawel: Wykaz,ze w dowolnym trojkacie stosunek sumy kwadratow dlugosci jego sroskowych do sumy
| | 3 | |
kwadratow dlugosci jego bokow rowna sie |
| |
| | 4 | |
25 wrz 11:55
Bogdan:
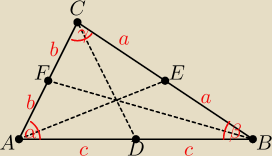
|CD| = d, |AE| = e, |BF| = f,
Z twierdzenia cosinusów:
| | −4a2+4b2+4c2 | | −a2+b2+c2 | | 4b2+c2−d2 | |
cosα = |
| = |
| i cosα = |
| |
| | 8bc | | 2bc | | 4bc | |
| −a2+b2+c2 | | 4b2+c2−d2 | |
| = |
| ⇒ d2 = 2a2 + 2b2 − c2 |
| 2bc | | 4bc | |
analogicznie cosβ = ... ⇒ e
2 = ... i cosγ = ... ⇒ f
2 = ...
| | d2 + e2 + f2 | |
następnie obliczamy |
| |
| | 4a2 + 4b2 + 4c2 | |
25 wrz 13:58
pigor: .., lub
jeśli
a, α, sa − dł.boku, m.kąta, dł.środkowej tego boku odpowiednio,
to 2x z tw. cosinusów w danym Δ i jednym z podziału przez s
a np.:
b
2=a
2+c
2−2accosβ i s
a2=
14a
2+c
2−accosα /*4 ⇒
⇒ 2accosβ= a
2+c
2−b
2 i 4s
a2= a
2+4c
2−2(a
2+c
2−b
2) ⇒
⇒
4sa2= 2b2+2c2−a2 i przez analogie masz :
4s
b2= 2a
2+2c
2−b
2
4s
c2= 2a
2+2b
2−c
2 , 3 równości, które dodając stronami dają ci
zależność (równość): 4(s
a2+s
b2+s
c2)= 4(a
2+b
2+c
2)−(a
2+b
2+c
2) ⇔
⇔ 4(s
a2+s
b2+s
c2)= 3(a
2+b
2+c
2) / : 4(a
2+b
2+c
2) ⇔
| | sa2+sb2+sc2 | | 3 | |
⇔ |
| = |
| c.n.w. ...  |
| | a2+b2+c2 | | 4 | |
25 wrz 14:47
Bogdan:
coś nowego pigorku wniosłeś do rozwiązania, które pokazałem?, toć to to samo, ale
bardziej złożone rachunkowo, bo z ułamkami
25 wrz 14:58
pigor: ..., ...
no tak masz rację, znasz mnie, ale to 2a itp. trochę
mi mieszało w głowie dlatego tu wolałem standard w oznaczeniach
choć nie lubię ułamków ; no i chciałem także mieć całe
rozwiązanie w ...
swojej szufladzie . ...
25 wrz 15:08
pigor: zauważ, że ułamek pojawił się u mnie tylko raz; pozdrawiam
25 wrz 15:10
Pawel: Dzieki.
25 wrz 17:56