f.liniowa asdf: rozwiąż algebraicznie i graficznie układ równań |x|+|y|=4 |x|−|y+1|=1

5-latek: A jak rozwazywaliscie takie przyklady na lekcji ? Nie wierze ze nie rozwiazywaliscie podobnych przykladow Podpowiedz albo wyznacz |x| z 1 rownania i podstaw do drugiego i go rozwiaz i wroc do podsatwienia albo odejmij 1 rownanie od drugiego i dalej rozwiazuj

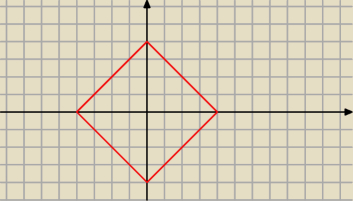
MQ: Pierwsze: |x|+|y|=4 to zbiór wszystkich punktów, których suma odległości od osi jest równa 4. Wystarczy więc sobie narysować to dla I ćwiartki (gdzie x>0 i y>0) i poodbijać symetrycznie na pozostałe. Wychodzi coś takiego jak na rysunku:

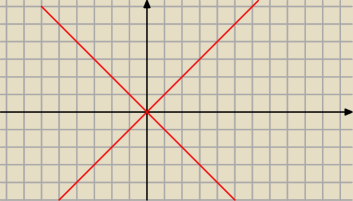
MQ: Drugie: To zadanie rozpatrzymy etapami: 1 etap: |x|−|y|=0 wtedy masz sytuację, jak na rysunku powyżej − to chyba zrozumiałe, bo x i y co do wartości bezwzględnej muszą się równać. Drugi etap na następnym rysunku , w następnym wpisie.

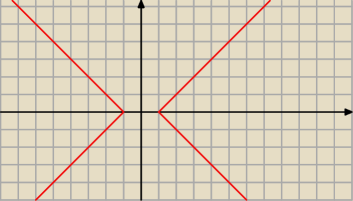
MQ: Drugie: 2 etap: |x|−|y|=1 Teraz x musi być równe co najmniej 1, więc nasz krzyż trzeba symetrycznie rozsunąć o ±1 wzdłuż osi OX Masz to na rysunku:

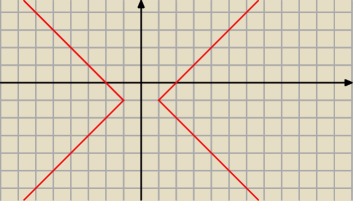
MQ: Drugie: 3. etap: |x|−|y+1|=1 Teraz już prosto, bo skoro mamy |y+1|, to oznacza to przesunięcie wzdłuż osi OY o wektor [0,−1], bo |y+1|=|y−(−1)| Dostajemy więc ostatecznie wykres, jak na rysunku: