f.log. Blue: Mam pytanko: Jak rysuję wykres funkcji log₂(|x|+4), to rysuję najpierw log₂|x| i przesuwam potem o 4 jednostki w lewo?

Kacper: nie

Kacper: dlaczego?

Blue: to jak to narysować?o.O

Piotr 10: Musisz wpierw zrobić translację o wektor u^→=[−4;0] , a następnie WB_OY

Aś: najpierw log₂ x przesuwasz o 4 w lewo a potem przekształcenie |x|

Blue: ahaaa... czyli najpierw wektor, a potem odbijam, tak?

Blue: Mi się to zawsze myli, co najpierw

Piotr 10: Tak. A jak będzie wyglądało, gdy log₂(Ix+4I) ?

Mila: 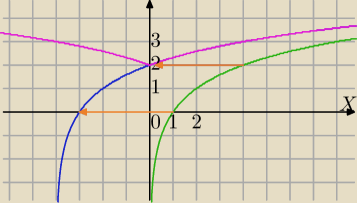y=log₂(x)→T_[−4,0]→y=log₂(x+4)→S_{OY dla x≥0} →y=log₂(|x|+4)

Eta: @ Blue Możesz zawsze wybrnąć .... rozpatrując funkcję przedziałami dla x≥0 f(x)= log₂(x+4) i dla x<0 f(x)= log₂(−x+4)

Blue: aha Piotr, czyli wtedy będzie, tak, jak myślałam Eta, w sumie racja Dziękuję wszystkim

Blue: Eta, nadal mam problem z tym rysowaniem... rozwiązałam przed chwilą kilka zadań i próbowałam tak rozpisać przedziałami, ale i tak się mylę, jak to rysować. Wiem, że to może głupia prośba, ale mogłabyś mi to jeszcze jakoś wytłumaczyć?

Eta: Hej Blue Teraz muszę na godzinkę wyjść z domu umiesz narysować wykres y= log₂(x+4) ....... dla x≥0 ( i zaznacz tylko tę część wykresu po prawej stronie dla x≥0 teraz narysuj wykres y=log₂(−x+4) .... dla x<0 ( zaznacz tylko tę część wykresu po lewej stronie dla x<0 i ostatecznie wykres zadanej funkcji z modułem (to te obydwie części w/w wykresów będę za godzinę

Mila: Przeanalizuj wpis 20:18

Eta:

Blue: Ja już rozumiem, że po prostu najpierw mam narysować dla x≥0 pomijając wartość bez., a potem tak jakby "odbić", ale wiecie, ja to tak na pamięć raczej robię, a nie umiem tego sobie logiczne wytłumaczyć (tego x mniejszego od zera) i boję się, że to zapomnę...

5-latek: To moze zawsz miej przed oczami definicje wartosci bezwzglednej