Równanie wykładnicze z parametrem.
Benedykt: Dla jakiej wartości parametru m (m E R) równanie
| | x + 6 | | 1 | |
∥ |
| ∥*** = ( |
| )m+5 ; |
| | x + 3 | | 4 | |
ma więcej rozwiązani ujemnych niż dodatnich? x≠ −3
*** "∥ "to zwykły moduł pojedynczy
Nie wiem nawet jak to ugryźć

/
23 wrz 23:21
MYSZ: | | x+6 | |
narysuj wykres funkcji | |
| | |
| | x+3 | |
wiecej rozwiazan ujemnych niz dodatnich bedzie powiedzmy w przedziale od a do b, to
rozwiazujesz
23 wrz 23:24
Benedykt: dzięki wielkie

23 wrz 23:26
5-latek:
| | x+6 | |
Taka funkcja y= |
| jest to funkcja wymierna |
| | x+3 | |
Przeksztalcmy ja do postaci kanonicznej (ja wole dzielic ) ale mozna to zrobic tak
| | x+3+3 | | x+3 | | 3 | | 3 | |
y= |
| = |
| + |
| = |
| +1 |
| | x+3 | | x+3 | | x+3 | | x+3 | |
| | |x+6| | | 3 | |
czyli |
| =| |
| +1| |
| | |x+3| | | x+3 | |
| | 3 | |
Wykres takie funkcji f(x)=y= |
| +1 przecie potrafisz narysowac i na to nakladasz wartosc |
| | x+3 | |
bezwzgledna (czyli te czesc wykresu krtora jest pod osia oX odbijasz nad os OX )
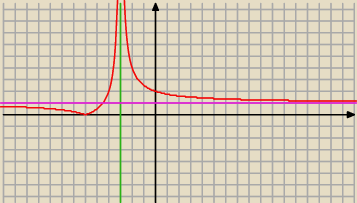
To jest juz ten wykres po nalozeniu wartosci bezwzglednej
23 wrz 23:39
 /
/

