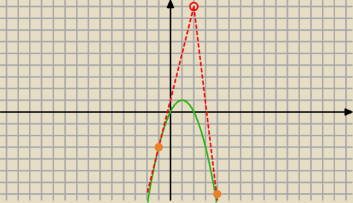
Wyznacz równanie stycznej do wykresu funkcji Piotrek: Wyznacz równanie stycznej do wykresu funkcji f(x)=−x2+2x, przechodzącej przez punkt P=(2,9)

Piotrek: Proszę o wykonanie

5-latek: https://matematykaszkolna.pl/strona/379.html

Piotrek: W przykładzie mam podane x0, tutaj punkt P. Jednak bym prosił o jakieś głębsze wyjaśnienie

===: ... to może zinterpretuj pojęcie styczna do funkcji −

===: równanie pęku prostych przez punkt P y−9=a(x−2) ⇒ y=ax−2a+9 styczna ma jeden punkt wspólny z kzywą −x²+2x=ax−2a+9 −x2+2x−ax+2a−9=0 Δ=0 (2−a)²+4(2a−9)=0 itd −

===: 4−4a+a²+8a−36=0 a²+4a−32=0 Δ₁=16+128 √Δ=12 a₁=−8 a₂=4

Piotrek: y−9=a(x−2) Wytłumacz mi dlaczego tutaj pojawia się "a" po prawej stronie

===: ostatecznie: y=−8(x−2)+9 ⇒ y=−8x+25 y= 4(x−2)+9 ⇒ y= 4x+1

===: a jaki znasz wzór na prostą przechodzącą przez punkt?

Piotrek: dzięki, ale prosze również o wyjaśnienie tego co napisałem wyżej

Piotrek: Okej, pojęte.

===: nie znasz wzoru: y−y_p=a(x−x_p) ?

===: −

Piotrek: o godzinie 22:53 już poznałem, ciężko z moją pamięcia do wzorów, a troche ich jest ^^ Wiem, wiem, że jest prosty

pitrek: fajne