Wykaż Adam: Wykaż, że w trójkącie, w którym |∡| = C, |BC| = a i |AC| = b, długości dwusiecznej kąta C jest

	√3 * a * b
równa
	a + b

bdziumzde5: ∡ = C ? bo dlugosc dwusiecznej bedzie zalezala od tego kata, a skoro w liczniku jest √3 to pewnie chodzi o 60⁰. Zgadza sie ?

Adam: Też mi się tak wydaje. Tylko o co chodzi?

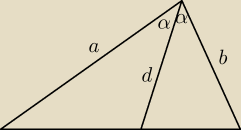
bdziumzde5: d − dl. dwusiecznej. P_ΔABC = P_ΔACD + P_ΔbCD

	sin a
1/2 ( ad*sin a + bd sin a ) = 1/2 ab sin 2a = 1/2 * ab * 2 *sin a * cos a /
	2

ad + bd = 2ab * cos a d ( a + b ) = 2 ab * cos a

	2ab cos α
d =
	a + b

dla α = 30⁰ ( wiec dla C = 60⁰ ) d = √3ab/(a+b)

Adam: EDIT: W poleceniu powinno być kąt C = 60 stopni

Adam: Hah, podałem nie do końca dobre polecenie a i tak to ogarnąłes Dzięki

bdziumzde5: dla c=60 masz latwiej, bo nie musisz znac wzoru na sin2α

Adam: to bez tego jakby to wyglądały w uproszczeniu zebym nieee przekombinował?

bdziumzde5:

a*d*sin 30		b*d*sin 30		a * b * sin 60
	+		=
2		2		2

1   a*d*   2		1   b*d*   2		√3   a*b*   2
	+		=		/ *4
2		2		2

ad + bd = √3ab d(a+b) = √3ab => d = ...