trojkaty bdziumzde5: 1) Wykaż, że jeśli α,β,γ są miarami kątów trójkąta, to

	α		β		γ		r
sin		* sin		* sin		=		, gdzie r,R oznaczaja odpowiednio promienie
	2		2		2		4R

okręgów: wpisanego w trójkąt i opisanego na trójkącie.

	BD		√3
2) Punkt D jest środkiem boku AC trojkata ABC. Majac dane		=		i
	AB		4

	π
i ∡BDC =		oblicz miarę kąta ABD.
	2

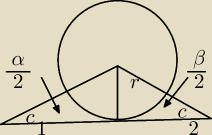
PW: 1) Wskazówka: Środek okręgu wpisanego jest wspólnym punktem dwusiecznych kątów trójkąta, zatem dla boku AB podzielonego punktem styczności na dwa odcinki c₁ i c₂ maja miejsce równości:₁

	c1		α		c2		β
		= ctg		,		= ctg		,
	r		2		r		2

skad

	c1		c2		α   cos   2		β   cos   2
		+		=		+
	r		r		α   sin   2		β   sin   2

	c1+c2		β   α   β   α   sin cos +cos sin   2   2   2   2
		=
	r		α   β   sin sin   2   2

	c		α+β   sin   2
		=		.
	r		α   β   sin sin   2   2

Zastosowanie analogicznych związków dla pozostałych boków i podstawienie ich do równości

	abc
sinα·sinβ·sinγ =
	8R3

wynikającej z twierdzenia sinusów powinno − po "pogłówkowaniu" − dać tezę. Przyjemnej pracy.

bdziumzde5: Dzieki ! Zaraz sprobuje dokonczyc.

ppb: Superancko, wszystko gra. Drugie zadanko tez zrobilem tym samym spodobem co wczesniej kilka razy probowalem, ale wczesniej bledy rachunkowe przeszkodzil Dzieki jeszcze raz.

Bdziumzde5: Superancko, wszystko gra. Drugie zadanko tez zrobilem tym samym spodobem co wczesniej kilka razy probowalem, ale wczesniej bledy rachunkowe przeszkodzil Dzieki jeszcze raz.