zapisz wzór funkcji linowej pudziu: Napisz wzór funkcji liniowej f, której wykres przechodzi przez punkt A( √3;5) i jest nachylony

	√3
do osi OX pod takim kątem α, że cosinus α =		. Podaj wzór proporcjonalności
	√7

prostej, której wykres jest równoległy do wykresu funkcji f.

Janek191:

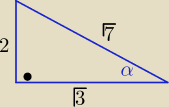
	√3		3
cos α =		⇒ cos2α =
	√7		7

	3		4		2
sin2 α = 1 −		=		⇒ sin α =
	7		7		√7

więc

	sin α		2		√3		2
tg α =		=		:		=
	cos α		√7		√7		√3

Mamy więc

	2
a = tg α =
	√3

czyli

	2
f(x) = a x + b =		x + b
	√3

Wykres funkcji f przechodzi przez punkt A = ( √3 ; 5), więc

	2
5 =		*√3 + b ⇒ b = 5 − 2 = 3
	√3

	2
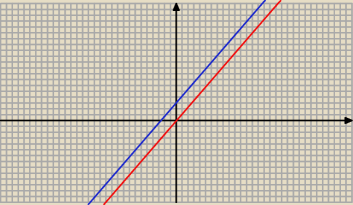
f(x) =		x + 3 − wykres koloru niebieskiego
	√3

==============================

	2
g(x) =		x
	√3

mix:

	2		2√3
y=a(x−√3)+5 a= tgα=		=
	√3		3

	2√3		2√3
k : y=		(x−√3)+5 ⇒ y=		*x +3
	3		3

	2√3
p∥k to p: y=		*x
	3