Rozwiąż Adam: 1. Narysuj wykres funkcji y=3^x. Wykorzystując uzyskany wykres narysuj wykres f(x)=|3^x+2−3|. Ile rozwiązań ma równanie f(x)=4m−3 w zależności od parametru m. 2. a) 4^x − 3 * 2^x − 40 > 0 b) (¹₃)^x2 * 3^3x−5 = ¹₂₇ c) 2^x+3 − 2^x = 112 d) 9^x+4 = 7^2x+8 e) (¹₃)^3x+2 ≤ ¹₂₇ Jeśli wiecie jak zrobić chociaż 1 przykład będę bardzo wdzięczny

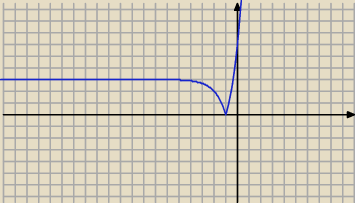
Kejt: 1. mając wykres 3^x... aby uzyskać wykres 3^x+2 przesuwamy 3^x o dwie jednostki w lewo. potem aby uzyskać 3^x+2−3 przesuwamy wykres o trzy jednostki w dół a następnie aby uzyskać |3^x+2−3| odbijamy wykres od osi x (tak żeby funkcja nie przekraczała osi x i była tylko dodatnia/równa zero) a dalej..: mając wykres, widać, że równanie będzie miało jedno rozwiązanie dla m.in. 4m−3 = 0 i tak dalej dopisz kiedy 2, a kiedy 1.

Janek191: z.2

	1		1
(		)x2*33 x − 5 =
	3		27

3 ^{− x2}*3 ^{3 x − 5} = 3⁻³ 3 ^{− x2 + 3 x − 5} = 3⁻³ − x² + 3 x − 5 = − 3 − x² + 3 x − 2 = 0 x² − 3 x + 2 = 0 ( x − 1)*( x − 2) = 0 x = 1 lub x = 2 ===============

Kejt: 2. a) podstawienie: t = 2^x => t² − 3t − 40 >0 b) pozamieniaj wszystko tak aby w podstawie było 3. c) wyłącz 2^x przed nawias i podziel przez tę drugą część d) zauważ, że 2x+8 = 2(x+4) e) zamień tak aby 3 było w podstawie.

Janek191: z.2 2 ^{x + 3} − 2 ^x = 112 2³*2^x − 2^x = 112 2^x*( 8 − 1) = 112 / : 7 2^x = 16 x = 4 ====

Adam: Dzięki jużmam gotowca na jutro :3