Wykres funkcji Metis: Mam taki wykres funkcji: g(x) = 4−(x−2)² −(x−2)²+4 Rozpoznaję funkcję f(x) = x² Następnie przekształcam g(x+a) Otrzymuję: (x−2)² Krok II g1(x)+a (x−2)²+4 I co teraz z − ? Dotyczy on f(−x) czy −f(x) I 2 pytanie: Jak po narysowaniu wykresu szybko sprawdzić na podstawie wzoru czy jest dobrze narysowany ? Wybieram punkt z wykresu np. : A(X1,Y1) i podstawiam do wzoru: y1=(x1−2)²+4 ?

MQ: Tu po lewej masz przycisk [ rysuję ] Wprowadź układ współrzędnych, napisz prawą stronę równania i masz wykres.

jakubs: Nie prościej narysować sobie ? : 1. (x−2)² 2. Odbić względem OX 3. Podnieść wykres o 4 do góry.

zzzz: dziwnie rozwiazujesz. to jest zwykla kwadratowa funkcja.

Metis: Na teście nie będę mógł rysować wykresów komputerowo Wszystkie przekształcenia musze rozpoznać na podstawie wzoru wyjściowego...

Saizou : a jeszcze łatwiej narysować g(x)=(x−2)²−4 W(2:4) h(x)=−g(x)=−(x−2)²+4

Metis: jakubs nawet jeśli narysuje sobie do momentu podniesienia wykresu o 4 do góry to nie będę wiedział jak narysować kolejny krok − odbić sym. wzgledem OX / OY?

Saizou : f(−x) symetria względem osi Y −f(x) symetria względem osi X

jakubs: Tak jak napisałem w 2 korku, odbić względem OX(http://matma.prv.pl/przeksztalcenia.php), a taki wykres jest bardzo prosto odbić. Później już wystarczy ten nowy wykres z 2 kroku podnieść o 4 do góry.

jakubs: Poprawka linka: http://matma.prv.pl/przeksztalcenia.php

Metis: Ok Rozjaśniło mi się. A II pytanie ?

jakubs: Jeżeli jest to kwadratowa, to ja zawsze sprawdzałem sobie wierzchołek, miejsca zerowe(o ile były) i znak przed x².

Metis: I jeszcze taki podpunkt: Dla jakich wartości parametru m równanie: |4−(x−2)²|=m+3 ...ma 3 rozwiązania... Jak to rozpatrzyć?

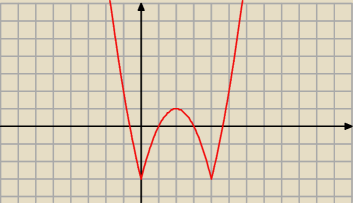
Saizou : Najłatwiej narysować funkcję f(x)=l4−(x−2)²l−3 no i poprzecinać ten wykres prostą y=m i dla jakiego m funkcja i prosta mają 3 punkty wspólne?

Piotr 10: A nie lepiej I4 − (x−2)²I = f(x) Cyba, że ktoś lubi bawić się i rysować Ale w sumie tam od razu dla 'm' będą rozwiązania, a tutaj dla k=m+3

Saizou : Piotrze to już jak kto woli, ale przesunięcie góra dół nie jest trudne xd

Piotr 10: Noo, ale teraz kwestia czy Metis umie narysować taki wykres. Jak nie to ja wczoraj podobny wykres pokazywałem jak rozwiązać

Metis: Jutro będę musiał wszystko rysować Saizou Powiedz mi jak to poprawnie zapisać Jeżeli m+3=0 to równanie ma 3 rozwiązania, m+3=0 ⇔ m=−3

Saizou : • Jeśli sugerowałeś się moim rysunkiem to dla y=1 (czyli dla m=1) mamy 3 rozwiązania • Natomiast jeśli rysowałeś tak jak proponuje Piotr czyli f(x)=l4−(x−2)²l to prosta jest określona wzorem y=4, ale tutaj wyraża się ona wzorem y=m+3, zatem 4=m+3 →m=1

Metis: Piotr wyjaśnij mi swój sposób

Metis: Dlaczego y=4

Piotr 10: Rysujemy wpierw wykres funkcji f(x) = |4−(x−2)²| Umiesz narysować jak nie to pisz m+3=k I teraz rysujemy tak odręcznie proste równoległe do osi X. Liczba przecięć z tą prostą określa liczba rozwiązań w zależności od k I przypuśćmy da k < 2 mamy zero rozwiązań. Więc teraz szukamy dla jakich 'm' k=m+3 , k< 2 m+3 < 2 m < − 1

Piotr 10: A i tak dodatkowo k∊R

Piotr 10: A która klasa 1 czy 2 ?

Saizou : można też algebraicznie (choć nie lubię tego sposobu) l4−(x−2)²l=m+3 (oczywiście żeby były jakiekolwiek rozwiązania to m+3≥0⇒m≥−3) l−x²+4xl=m+3 (po redukcji wyrażeń pod modułem) −x²+4x=m+3 lub −x²+4x=−m−3 x²−4x+m+3=0 lub x²−4x−m−3=0 Δ₁=4−4m lub Δ₂=28+4m no i teraz mamy takie kombinacje że Δ₁=0 i Δ₂>0 lub Δ₁>0 lub Δ₂=0 (na razie pomijamy przypadek że pierwiastki mogą być takie same ) Δ₁=4−4m=0⇒m=1 i Δ₂=28+4m⇒m>−7 (a z założeni mamy że m≥−3 to oznacza że tym bardziej Δ₂>0) czyli rozwiązaniem byłoby m=1 a teraz drugi przypadek Δ₁>0⇒m>1 Δ₂=0⇒m=−7 (a z założeń m≥−3), zatem ten przypadek jest niemożliwy no ale co z pokrywającymi się pierwiastkami? Zróbmy więc sprawdzenie dla m=1. Podstawiając do wyjściowego równanie l−x²+4xl=1+3=4 −x²+4x=4 lub −x²+4x=−4 x²−4x+4=0 lub x²−4x−4=0 (x−2)²=0 lub (x−2+2√2)(x−2−2√2)=0 zatem są 3 różne pierwiastki, czyli rozwiązanie to m=1

Metis: Początek II ale dział z I klasy. Analizuje sobie to co napisałes

Metis: Saizou twój sposób dla mojego poziomu odpada

Metis: Piotrze Możesz rozpisać mi jak to będzie poprawnie wyglądało dla mojego przypadku ? http://wstaw.org/m/2014/09/21/wykres.png A narysować to narysuje

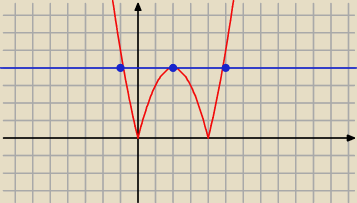
Saizou : Wyrobisz się narysujmy nasz wykres f(x)=l4−(x−2)²l •zaczynamy rysować od f(x)=x² •następnie przesuwamy f(x) o 2 jednostki w prawo h(x)=(x−2)² •teraz symetria względem osi X g(x)=−h(x)=−(x−2)² (przed całym wyrażeniem dajemy −) • przesuwamy o 4 jednostki w górę k(x)=−(x−2)²+4=4−(x−2)² • nakładamy wartość bezwzględną (czyli to co pod osią x wędruje symetrycznie nad oś X) l(x)=l4−(x−2)²l na tym byś zakończył rysowanie sposobem Piotra teraz patrzymy dla jakiej prostej mamy 3 punkty wspólne, wychodzi nam że wzór jej to y=4, zale dla nas y=m+3, zatem 4=m+3, czyli m=1

Piotr 10: Dzięki Saizou

Metis: No ja też dziękuje

Saizou : myślę że zrozumiale to napisałem

Metis: Tak , tak. Czaje wszyściutko. Teraz kolejne pytanie. Jak myślicie jeżeli będę miał wyznaczyć zbiór rozwiązań nierówności za pomocą wykresów odpowiednich funkcji a wyznacze je algebraicznie to będzie źle

Saizou : tak to jest błąd, bo nie stosujesz się do polecenia zadania, możesz dostać punkty jedynie za wynik, a nie za tok rozumowania

Metis: Jak ja to wszystko rozrysuje w ciagu 45 minut Na przykład takie zadanie: Na podstawie znanych Ci wykresów funkcji wyznacz zbiór rozwiązań nierówności: l(x − 1)² − 4l > x+1

Metis: Narysowałem: http://wstaw.org/m/2014/09/21/wykres2.png I jak teraz będzie wyglądał zapis

Saizou : rysujemy y=x+1 (to proste po kratkach na skos funkcja rosnąca, przecina os Y (0;1)) g(x)=x² zróbmy przesunięcie od razu o 1 w prawo i o 4 w dół (czyli tzw. translacje o wektor [1;−4], przenosimy najlepiej punkty kratowe czyli takie gdzie się nam kratki przecinają) i otrzymamy h(x)=(x−1)²−4 a teraz nakładamy wartość bezwzględną, czyli to co pod osią x wędruje symetrycznie nad osi X

Saizou : a teraz musimy odczytać kiedy wykres wartości bezwzględnej jest nad wykresem prostej, tzn dla jakich X to zachodzi

Metis: Nie widzę tego Szukałem u Pazdry, ale też nie ma takiego przykładu przedstawionego.

Saizou : l(x−1)²−4l umiesz to narysować?

Metis: Tak tak. Narysować narysuje , ale nie widzę tego po narysowaniu obu wykresów. Tzn kiedy ten wykres jest nad wykresem prostej.

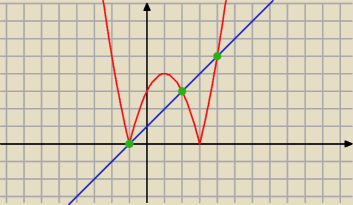
Saizou : kiedy czerwony wykres jest nad niebieskim ?

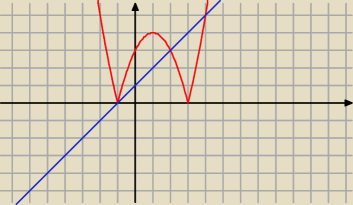
5-latek: Taki Ci wykres wyszsedl ?

5-latek: Czesc Saizou

Saizou : Witam Cię, 5−latku

Metis: Saizou zapisz mi kiedy czerwony wykres jest nad niebieskim, muszę sobie to przeanalizować bo pierwszy raz się z tym spotykam.

Saizou : dla x∊(−∞:−1)∪ (1:2) ∪ (4:+∞)

Metis: Dzięki! Jak bede miał kolejne pytania to będe pisał

Saizou : spoko, jak będę umiał pomóc to pomogę

Metis: Ostatnie na dzisiaj Mam nadzieje że dobrze przygotowałem się do sprawdzianu. Na pods. wykresów odp. funkcji wyznacz zbiór rozw nierówności

	4
4−|a−2| >
	3−a

Metis: I wykres: Rozpoznaje |a| przesuwam o 2 w prawo > |a−2| , przesuwam o 4 w góre |a−2|+4 odbijam symetrycznie > −|a−2|+4 II wykres

	1		1
Rozpoznaję		, przesuwam o 3 w lewo >		> nie wiem co z licznikiem >i ostatni
	a		a+3

krok (−x)

Metis: Wykres: http://wstaw.org/m/2014/09/21/wykres3.png I jak w tym przypadku wskazać rozw?

jakubs: Moja propozycja do drugiego:

	−4
1.
	a

	−4
2. Przesuwasz o 3 w prawo i otrzymujesz
	a−3

jakubs: Na rysunku wszystko widać pomyśl

Metis: x∊(−∞,2) u (7,+∞)

Metis: x∊(−∞,2) u (−1,2) u (7,+∞)

jakubs: Według mnie: (−1,2)∪(3,7)

jakubs: Wolfram potwierdza: http://www.wolframalpha.com/input/?i=-4%2F%28x-3%29%3C4-|x-2|

Metis: Ok już czaję Zadaję sobie pytanie kiedy I wykres leży nad II wykresem. I wychodzi. Dzięki!

jakubs:

Saizou : Metis i jak kartkówka?

Metis: Cześć Saizou Kartkówka poszła nieźle Dostałem zadania bardzo podobne do tych, których przykłady przerabiałem tutaj. Dwa zadanka prawie identyczne treścią. Inne wykresy funkcji i zamiast odnalezienia dla jakich wartości parametru równanie ma 3 rozwiązania miałem przeprowadzić dyskusję−ale to analogicznie do tego co mi napisałeś A wykresy były mniej skomplikowane do narysowania niż te której tutaj pokazywałem. Jedyne czego nie udało mi się zrobić to narysować wykres parametru m w zależności od liczby rozwiązań(czy jakoś tak ). Odejdą mi jeszcze gdzieś pewnie pkt za zapis. Dziękuje Tobie , jakubsowi i Piotrowi za pomoc Myśle, że jakaś trójczyna/czwórczyna będzie

jakubs: Będzie dobrze, ja 3 klasę LO zaczynałem na 3 i 4, a 10 ostatnich ocen w kwietniu na e−dzienniku to były same 5 i 6. Oceny to nic, bo i tak matura najważniejsza i tego się trzymaj

Piotr 10: Ja niestety 3

Saizou : ooo... to gratulacje, ale może być lepiej. Wykres f(m) to takie schodki, wzór funkcji zazwyczaj prezentuje się następująco { 0 dla m∊... f(x)= 1 dla m∊.... { 2 dla m∊.... i tak dalej, no i powstają schodki, bo jak by spojrzeć to f(m)=a ,gdzie a∊R to są proste równoległe do osi X, ale obcięte dla przedziałów xd

Saizou : a tutaj jeszcze cenna uwaga dotycząca oznaczeń osi, oś Y to f(m) a oś X to m

Metis: 3 i 4 u mojego nauczyciela z matmy są ok , tym bardziej że nie daje identycznych zadań jakie robiliśmy na lekcji, poza tym szuka dziury w całym... (ale podobnie jak wszyscy matematycy ) Ocen będzie dużo, bo w ciągu tygodnia mam 8 lekcji matematyki A dyskusję przeprowadziłem słownie 1). Gdy m=... to równania ma... itd.

Saizou : to jest okej, ale najlepiej to pisać przy pomocy wzoru xd

Metis: Od następnego sprawdzianu będzie ze wzorem

Saizou : ok, ok, już trzymam kciuki

Metis: Dzięki Będzie dobrze