Funkcja kwadratowa jureł: Proszę o dokładne rozwiązanie z komentarzem: Dla jakich wartości parametru m równanie !x²−9! + !x²−16!=m ma dokładnie dwa rozwiązania Wartość bezwzględna to !.

PW: Nie, „!” to silnia. Znak wartości bezwzględnej znajduje się w zestawie znaków i jest dostępny z klawiatury numerycznej jako Alt0124 (włączony NumLock, wciśnięty i przytrzymany lewy Alt, wstukane 0124, zwolniony Alt). Dla wzroku nierozróżnialna jest mała litera "L', której przy tej czcionce można użyć w zastępstwie znaku wartości bezwzględnej.

jureł: ok dzięki

PW: Wskazówka: funkcja po lewej stronie równania jest parzysta, f(−x) = f(x), wystarczy zatem rozwiazać równanie dla x > 0. Jeżeli liczba x₀ > 0 jest rozwiązaniem, to drugim rozwiązaniem jest liczba −x₀. Zacznij więc od narysowania parabol y=x²−9 oraz y=x²−16 − w jednym układzie współrzędnych, tylko dla x >0 i ustal przedziały, na których obie są nieujemne, obie ujemne oraz "jedna tak, druga inaczej". Trzeba będzie rozwiązać trzy równania na trzech przedziałach.

jureł: A rozwiązanie tego na 4 przypadki: obydwa dodatnie, ujemne, jedno dodatnie jedno ujemne, jedno ujemne jedno dodatnie?

PW: A narysowałeś tak jak radziłem?

jureł: Narysowałem funkcje, natomiast nie wiem jak oznaczyć te przedziały

PW: Pionowe kreski w miejscach zerowych pokażą.

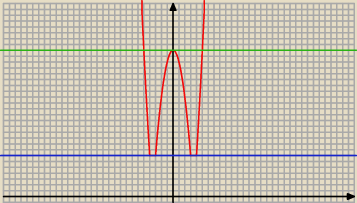
MQ: Można też podstawić y=x² i szukać liczby rozwiązań dla y, z dodatkowym warunkiem y≥0 Po podstawieniu dostaniemy sumę odległości od pkt. 9 i 16. I mamy 3 rozwiązania: 1. Jeżeli m< 16−9 czyli od odległości między tymi punktami, to nie ma rozwiązań dla y i tym samym dla x 2. Jeżeli m= 16−9, to mamy nieskończenie wiele rozwiązań dla y ⇒ dla x tak samo 3. Jeżeli m>16−9, to mamy dwa rozwiązania dla y, ale trzeba tu uważać, żeby jedno z rozwiązań dla y nie było ujemne, lub =0. Rozbijamy to więc na 3 przypadki: a) 16−9<m<16−9+2*9=16+9, wtedy oba punkty y leżą na dodatniej stronie osi ⇒ dla x 4 rozwiązania b) m=16−9+2*9=16+9, wtedy jedno rozwiązanie dla y=0 i jedno dla y>0 ⇒ dla x 3 rozwiązania c) m>16−9+2*9=16+9 wtedy jedno y<0 (to odrzucamy) i jedno y>0 ⇒ dla x 2 rozwiązania