Zadnie z ciągu arytmetycznego. patkiii: Pomocy! Zadnie z ciągu arytmetycznego. Uzasadnij, że każde dwa trójkąty prostokątne, których długości boków są kolejnymi wyrazami ciągu arytmetycznego, są podobne. Oblicz stosunek najkrótszego boku do najdłuższego.

Kacper: Co wiadomo o trójkącie prostokątnym?

patkiii: nic więcej nie podano

patkiii: jest wskazówka

patkiii: wskazówka; zauważ, że liczby a, a+r, a+2r tworzą ciąg arytmetyczny, a twierdzenie Pitagorasa dotyczy trójkątów prostokątnych.

Kacper: No właśnie o to mi chodziło.

patkiii: i jak wyszło coś

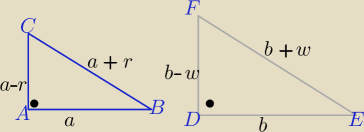
Eta: r, w −−różnice ciągów arytmetycznych r∊(0,a) i w∊(0,b) i a>0 i b>0 z tw. Pitagorasa: (a−r)²+a²=(a+r)² i (b−w)²+b²=(b+w)² a²−4ar=0 ⇒a=4r i b²−4bw=0 ⇒ b= 4w boki trójkątów : ABC: 3r,4r,5r i DEF : 3w, 4w,5w

	3r		4r		5r		r
zatem		=		=		=		−−− skala podobieństwa
	3w		4w		5w		w

zatem takie trójkąty są podobne c.n.u

patkiii: Dzięki Eta a jeszcze stosunek najkrótszego boku do najdłuższego? w odpowiedziach jest 0,6.

patkiii: Już wiem, przepraszam nie było pytania

patkiii: Eta, mam jeszcze jedno pytanko. Bowiem próbuje rozwiązać to zadanie, gdy za boki jednego trójkąta przyjmuję (a, a+r, a+2r), a za boki drugiego przyjmuję (b, b+w, b+2w). Jakoś nie chce mi wyjść

Ben Akiba: a przednie też wymaga pomocy

patkiii: nie, przednie nie.