 Przez środek wysokości stożka poprowadzono prostą równoległą do tworzącej długości k. Oblicz
długość odcinka będącego częścią wspólną prostej i stożka.
Przez środek wysokości stożka poprowadzono prostą równoległą do tworzącej długości k. Oblicz
długość odcinka będącego częścią wspólną prostej i stożka.
| 3 | ||
Odp. | k | |
| 4 |
 napisane jest również
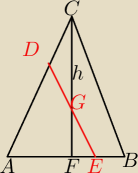
"Przekrojem stożka jest poniższy trójkąt równoramienny ABC. Podstawą trójkąta (|AB|) jest
średnica podstawy stożka, u nas jej długość oznaczymy jako a. Wysokość stożka to także
wysokość tego trójkąta (|FC|=h)." to jest zrozumiałe
ale nie wiem, czy dobrze oznaczyłem trójkąty prostokątne BCF i DGF
napisane jest również
"Przekrojem stożka jest poniższy trójkąt równoramienny ABC. Podstawą trójkąta (|AB|) jest
średnica podstawy stożka, u nas jej długość oznaczymy jako a. Wysokość stożka to także
wysokość tego trójkąta (|FC|=h)." to jest zrozumiałe
ale nie wiem, czy dobrze oznaczyłem trójkąty prostokątne BCF i DGF

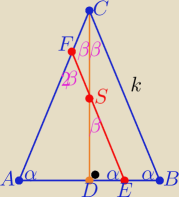 Wprowadź swoje oznaczenia ( nie mają wpływu na rozwiązanie !
|AB|=2r , |BC|=k EF|= x
z podobieństwa trójkątów DES i DBC z cechy (kkk)
Wprowadź swoje oznaczenia ( nie mają wpływu na rozwiązanie !
|AB|=2r , |BC|=k EF|= x
z podobieństwa trójkątów DES i DBC z cechy (kkk)
| r | ||
........ ⇒ |DE|= | ||
| 2 |
| 3 | ||
|AE|= | r | |
| 2 |
| x |
| 3 | ||||||||||
. | = | ⇒ x= | k | |||||||||
| k | 2r | 4 |