...
Hondziarz: Z wierzchołków podstawy AB trójkąta równobocznego o boku "a" rozpoczęły ruch dwa punkty.
Poruszają się one wzdłuż boków AC i BC z prędkościami odpowiednio v
1 i v
2. Po jakim czasie
odległość między nimi będzie równa wysokości trójkąta?
Pomocy
20 wrz 14:38
Kacper:
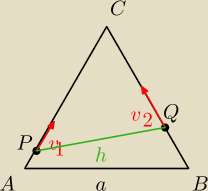
Ja umiem zrobić rysunek
20 wrz 14:58
Hondziarz: No ładny, ładny
To może zaraz pojawi się ktoś kto będzie umiał zrobić resztę zadania
20 wrz 15:02
Hondziarz: Ktoś ogarnia?
21 wrz 14:05
Hondziarz: Pomocy
22 wrz 17:08
Hondziarz: HELP
Podbijam to może ktoś zobaczy i pomoże.
23 wrz 16:53
Kacper: Co to w ogóle za przedmiot?
23 wrz 16:56
Hondziarz: Matematyka wbrew pozorom. To jest zadanie z Korespondencyjnego Kursu z Matematyki Politechniki
Wrocławskiej.
23 wrz 16:59
23 wrz 17:01
Kacper: Jakoś ja w tym momencie nie mam pomysłu. Może ktoś "starszy" stażem będzie widział jak.
23 wrz 17:05
Hondziarz: Oki. Dzięki za dobre chęci. Rysunek już zrobiłeś
23 wrz 17:08
Janek191:
I AP I = v
1*t
więc
| h1 | |
| = sin 60o = 0,5√3 ⇒ h1 = 0,5√3 v1*t |
| v1*t | |
a
1 = 0,5 v
1*t
oraz
| h2 | |
| = sin 60o = 0,5√3 ⇒ h2 = 0,5√3v2*t |
| v2*t | |
a
2 = 0,5 v
2*t
y = a − a
1 − a
2 = a − 0,5v
1*t − 0,5 v
2*t = a − 0,5*( v
1 + v
2)*t
x = h
2 − h
1 = 0,5
√3 v
2*t − 0,5
√3 v
1*t = 0,5
√3*( v
2 − v
1)
więc
I PQ I
2 = x
2 + y
2 = ....
23 wrz 17:25
Janek191:
Oczywiście I PQ I = 0,5
√3*a
23 wrz 17:28
Janek191:
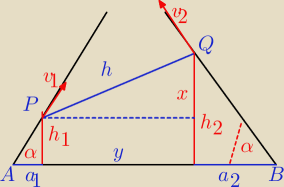
α = 60
o
23 wrz 17:35
Hondziarz: Dzięki wielkie
Zaraz nad tym posiedzę i postaram się zrozumieć
23 wrz 18:03
Hondziarz: Chciałbym wrócić do tego jeszcze. Jak podstawie pod to równanie co napisałeś to wychodzi
równanie kwadratowe. Jak je rozwiązać? Nie wiadomo nawet czy Δ jest dodatnia czy ujemna.
24 wrz 18:09
Hondziarz: Pomocy
Pilne na jutro
24 wrz 18:17
Kacper: Jak na jutro? Przecież to nie jest obowiązkowe
24 wrz 18:20
Hondziarz: Tak, ale jutro to wysyłam
24 wrz 18:28
Hondziarz: A wiesz o co chodzi w tym równaniu? Przecież t nie da się z niego wyznaczyć normalnie.
Przynajmniej ja nie wiem jak.
24 wrz 18:31
Kacper: Napisz to równanie jak wygląda
24 wrz 18:51
Hondziarz: Po uproszczeniu tak:
| | 3 | | (v1+v2)2 | | 1 | |
t2[ |
| (v2−v1)2+ |
| ]−a(v1+v2)t+ |
| a2=0 |
| | 4 | | 4 | | 4 | |
24 wrz 19:08
Kacper: równanie kwadratowe
24 wrz 19:11
Hondziarz: No to wiem, ale jak to zrobić? Rozpatrywanie przypadków jest bez sensu bo v1 i v2 mają stałe
wartości. To nie są parametry.
24 wrz 19:20
Kacper: niewiadoma to "t" a c
1 i v
2 to stałe
24 wrz 19:41
Hondziarz: Dobra zrobiłem to w końcu
24 wrz 20:19