prawdopodobieństwo geometryczne arli28: W kwadrat wpisano trójkąt tak, że podstawa trójkąta jest podstawą kwadratu, a trzeci wierzchołek dzieli przeciwległy bok kwadratu na połowy. W trójkąt ten wpisano koło. We wnętrzu kwadratu pojawia si losowo punkt M. Zakładając, że prawdopodobieństwo pojawienia się punktu M w dowolnym obszarze należącym do kwadratu zależy jedynie od miary tego obszaru, obliczyć prawdopodobieństwo, że punkt pojawi się w kole.

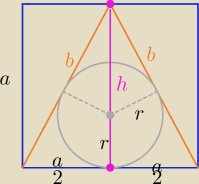
Eta: |Ω|= P(kwadratu)= a²

	a2		a		a2
h=a b=√a2+		=		√5 , P(Δ)=
	4		2		2

	2P(Δ)		a2		a
|A|=P(koła)= πr2 , r=		=		=		(√5−1)
	2b+a		a√5+a		4

	πa2
P(koła)= ......		(3−√5)
	8

	P(koła)		π
P(A)=		= ....... =		(3−√5)
	P(kwadratu)		8