c#1
Lukas:
jak wyznaczyć Dziedzinę funkcji i ją narysować
f(x)=√−(x+3)4
−(x+3)4≥0
Dwumian Newtona mam użyć ?
19 wrz 21:49
Lukas:
−(x4+3x3+9x2+27x+81)≥0
x4+3x3+9x2+27x+81≤0
Jak to namalować ?
19 wrz 21:54
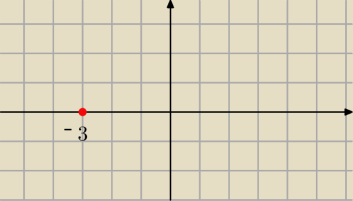
ICSP: D : x = −3
19 wrz 21:57
Mila:
czy pod pierwiastkiem jest?
−(x+3)4
19 wrz 21:57
Lukas:
tak
19 wrz 21:57
Lukas: ?
19 wrz 22:08
Mila:
To w takim razie to wyrażenie
−(x+3)4 ≤0
D;
tylko dla wartości zero pod pierwiastkiem możesz obliczyc wartość funkcji, w innym przypadku
masz wartość ujemną.
x+3=0⇔x=−3
19 wrz 22:11
Lukas:
Ale jak mam to rozwiązać ?
19 wrz 22:15
Mila:
Tak jak napisałam 22:11
−(x+3)4=0⇔
x+3=0
x=−3
19 wrz 22:21
Lukas:
Ale tam mam nierówność więc skąd znak ''='' ?
19 wrz 22:22
5-latek: −(x+3)4≥0 to (x+3)4≤0 −narysuj wykres tej funkcji
lub mozesz zapisac tak (x+3)2<=0 a to juz umiesz narysowac
19 wrz 22:25
Mila:
Ujemny wariant musisz odrzucić.
−(x+3)4≥0 /*(−1)
(x+3)4≤0
wiemy że (x+3)4 nie moze byc ujemne
Prawda?
Pozostaje mozliwość, że x+3=0
19 wrz 22:28
Lukas:
Nic nie rozumiem

Mimo chęci..
19 wrz 22:28
Mila:
Podstaw kilka wartości i oblicz wartość wyrażenia
−(x+3)2
dla 0, 1,−1, 2, −2,3,−3
19 wrz 22:38
Mila:
Dla :
−(x+3)4
19 wrz 22:39
Lukas:
Podstawiam:
dla x=1 −16
x=2 −25
x=3 −36
x=−1 −4
x=−2 −1
x=−3 0
19 wrz 22:42
Saizou :
funkcja f(x)=√x ma dziedzinę x≥0
zatem
g(x)=√−(x−3)4 ma dziedzinę −(x−3)4≥0 i musimy obliczyć tę nierówność
−(x−3)4≥0 /*(−1)
(x−3)4≤0 /4√
lx−3l≤0 kiedy wartość bezwzględna jest ≤0? (wiemy że lxl≥0, przy czym =0 zachodzi tylko
wtedy
kiedy wyrażenie w
module się zeruje )
zatem
x=3 i to jest naszą dziedziną, a teraz liczymy wartość dla argumentu x=3
g(3)=√−(3−3)4=√0=0
zatem wykresem tej funkcji jest punkt o współrzędnych (3:0)
19 wrz 22:44
Lukas:
Czyli trzeba było po prostu spierwiastkować.
Dziękuję, już wszystko jasne.
i wykresem jest punkt (3,0) ?
19 wrz 22:48
Mila:
Widzisz 22:42, że masz ujemne wartości, dla pierwiastka kwadratowego niedozwolone .
Tylko mozesz obliczyc pierwiastek z zera − w tym zadaniu.
.
19 wrz 22:50
5-latek: NIe bo Saizou sie pomylil zamiast −(x+3)4 napisal −(x−3)4
TY tylko poraw sobie
19 wrz 22:50
Mila:
W Twoim zadaniu:
(−3,0)
19 wrz 22:50
Saizou :
Faktycznie, ale to chyba
Lukas sam sobie poprawi

19 wrz 22:53
Eta: 
19 wrz 22:53
Lukas:
Wykres dziedziny x=−3 ?
19 wrz 22:55
Lukas: ?
19 wrz 23:06
5-latek:

Tak masz ja narysowac
19 wrz 23:11
Lukas:
?
19 wrz 23:52
Ajtek:
Tak to wygląda. Nie jest to wykres dziedziny, tylko wykres f(x) podanej na początku.
20 wrz 00:01
Lukas:
a ja napisałem wyraźnie wykres dziedziny

20 wrz 00:13
Ajtek:
Takie masz polecenie? Wykres dziedziny?
20 wrz 00:17
Lukas:
Tak

20 wrz 00:18
Ajtek:
Kurcze, dziwne

Ja nigdy nie rysowałem wykresu dziedziny, tylko wyznaczałem dziedzinę funkcji
i rysowałem jej wykres (funkcji, nie dziedziny)

.
20 wrz 00:22
Lukas:
A tutaj jest inaczej....
20 wrz 00:23
Ajtek:

Jeśli dziedzinę, to narysował to bym tak jak wyżej.
20 wrz 00:26
Lukas:
ale dziedzina to x=−3
podstaw sobie 1 i zobacz czy należy do dziedziny...
20 wrz 00:32
Ajtek:
A czy widzisz na moim wykresie kropkę przy x=1?
20 wrz 00:35
Ajtek:
Lucas, czy polecenie brzmi: Wyznacz dziedzinę funkcji i narysuj jej wykres?
20 wrz 00:37
Lukas:

up
20 wrz 22:00
Mila:
D={−3}
Masz narysować wykres f(x), Ajtek narysował 00:01.
20 wrz 22:03
Lukas:
Ja mam narysować wykres dziedziny. Nie funkcji f(x)
20 wrz 22:05
Mila:
To rysunek Ajtka 00:26 na osi liczbowej.
20 wrz 22:08
Lukas:

a nie w układzie wsp x=−3
20 wrz 22:10
Lukas:
up ?
23 wrz 22:06
Hajtowy: 
23 wrz 23:35
Mila:
Dziedzina funkcji jednej zmiennej (x) to zbiór liczb na osi OX.
W twoim przykładzie jest to zbiór {−3} jednoelementowy. Rysunek Ajtka jw.napisałam.
24 wrz 19:44
Eta:

Witaj
Mila 
24 wrz 19:50
Mila:
Witaj Eta, jakoś mniej Cię tu widuję. Chora byłaś?
24 wrz 20:43
Lukas:
Ale nadal nie rozumiem ?
24 wrz 20:44
Mila:
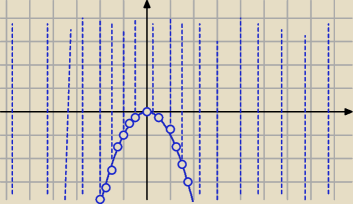
Rysunek : 00:26 na osi .
f(x)=
√−(x+3)4
D={−3}
f(−3)=
√−(−3+3)4=
√0=0
x=−3 argument
y=0 wartość funkcji.
Jeśli nie rozumiesz , to zostaw to i idź dalej.
W przypadku:
log
2(x
2+y)≤1 wyznaczamy dziedzinę
x
2+y>0 ( bo liczba logarytmowana jest dodatnia)
y>−x
2
W tym przypadku dziedziną jest zbiór punktów których współrzędne(x,y) spełniają warunek y>−x
2
,
to znaczy leżących w obszarze nad parabolą y=x
2
24 wrz 20:58
Lukas:
Mila dziękuję Ci bardzo za wyjaśnienie. Nie wiem jaki działy mam za bardzo robić i jestem
trochę w rozsypce. Proszę o radę
24 wrz 22:13
Eta:
planimetrię 
24 wrz 22:18
Mila:
Teraz w LO przerabiają potęgi i pierwiastki, funkcja wykładnicza, funkcja logarytmiczna,
równania wykładnicze, równania logarytmiczne.
24 wrz 22:19
Lukas:
I tak ogólnie ukrywałem to ale dostałem się na studia i będę studiował, ale nie to co chcę i
nie na tej uczelni której chcę...
A maturę muszę z R muszę napisać koniecznie żeby się dostać na wymarzone studia.
24 wrz 22:20
Lukas:
Potęgi i pierwiastki ok to zacznę od tego

24 wrz 22:25
Eta:
A ja znałam tę "tajemnicę"

24 wrz 22:25
Lukas:
Uniwersytet jednak daleki od Marynarki Wojennej.
Ale zawsze to coś. Wiem, że będzie trudno ale spróbuje.
24 wrz 22:26
Mila:
I to galopem , dodaj funkcje trygonometryczne.
I nie kłóć się z nami, tylko stosuj do rad, aby nie było wylotki.
Wytrwałości.
24 wrz 22:27
Eta:

24 wrz 22:28
Lukas:
Dobrze, będę słuchał się rad, Obiecuję.
Mogę codziennie siedzieć po 8h nad zadaniami

24 wrz 22:29
Eta:
Z godzinną przerwą na....
kisiel 
24 wrz 22:37
Lukas:
Pierwsze zadanie
oblicz
√6−3√3*(63+36
√3)
1/4
pierwszy człon wiem jak zrobić
24 wrz 22:38
Eta:
Łatwiej tak: włącz pierwszy czynnik pod pierwiastek stopnia 4
czyli podnieś go do potęgi 4 i szybko .......zobaczysz wynik
24 wrz 22:41
5-latek: Wlasnie zrobilem sobie wiśniowy

24 wrz 22:46
Lukas:
Pierwszy czynnik ?
Możesz pokazać jak to uczynić ?
24 wrz 22:46
Eta:
(√6−3√3)4= ..........
4√(...............) *(63+36√3)=.........
24 wrz 22:48
Eta:
Smacznego "małolatku"

kisiel jest dobry na stawy , kości i.....

24 wrz 22:49
Lukas:
Ale czemu mam to wciągać pod pierwiastek, skoro to nie jest pod pierwiastkiem ?
24 wrz 22:52
5-latek: Dziekuje

I..... wiem . Bede go teraz duzo potrzebowal

24 wrz 22:52
Eta:
a*4√ b= 4√a4*b ........ jasne ?
24 wrz 22:52
Eta:
No o to chodzi żeby było pod pierwiastkiem
Wykonaj to o czym mówię i zobaczysz ..... po co ?
24 wrz 22:54
Lukas: Tak, teraz jasne.
4√(√6−3√3)4(63+36√3)
24 wrz 22:55
Eta:
(√6−3√3)4=.......... oblicz
24 wrz 22:57
Lukas:
(6−3√3)2=63−36√3
24 wrz 23:00
Eta:
ok

24 wrz 23:01
Eta:
teraz dokończ .........
24 wrz 23:02
Lukas:
4√(6−3√3)2(6+3√3)2=4√36−37=4√9 ?
24 wrz 23:05
Mila:
9*3=27
24 wrz 23:17
Eta:
źle
4√(6−3√3)2*(6+3√3)2= ............
24 wrz 23:17
Eta:
......= √36−27=........
24 wrz 23:19
Eta:
No i jak? .......... żyjesz?

24 wrz 23:26
Metis: Podziwiam Was za tą cierpliwość

24 wrz 23:34
Mila:
Metis, co masz obecnie na lekcjach matematyki?
24 wrz 23:35
Metis: Milu, rozpoczynam funkcję liniową

24 wrz 23:36
Mila:
O, to wdzięczny dział.
24 wrz 23:37
Metis: Nie zdawałem sobie sprawy, że jest tak obszerny

U Pazdry − ponad 61 stron.
24 wrz 23:39
Eta:
No i
Lukas tak się miał uczyć, a................ poszedł lulu

24 wrz 23:54
5-latek: No i bedzie mu sie śnil

z tą trójką
24 wrz 23:59
Lukas:
żyję i dziękuję. Nie mogłem wejść bo miałem problemy z internetem
25 wrz 10:56
Lukas: ?
25 wrz 21:41
Eta:

25 wrz 22:06
Lukas: ?
25 wrz 23:19
Mila:
Zadanie dać?
25 wrz 23:20
Eta:
Dla mnie? ...


25 wrz 23:21
25 wrz 23:22
Lukas: Proszę jeszcze raz o wytłumaczenie czemu tam zrobił się pierwiastek stopnia 2
25 wrz 23:33
Eta:
4√a−b)2*(a+b)2 = 4√ [(a−b)*(a+b)]2 = [[(a−b)(a+b)]2]1/4= ..........
25 wrz 23:37
Mila:
[(36−27)2]14=(9)12=√9
25 wrz 23:38
Eta:
4√a2=√a
25 wrz 23:46
Eta:
Ej ..
Mila 
25 wrz 23:47
Eta:
Dobranoc

25 wrz 23:47
Eta:
100 moje

25 wrz 23:48
Lukas:
Dziękuję. Mogę jeszcze jedno zadanie wstawić ?
25 wrz 23:51
5-latek: Dobry wieczor Paniom

Ja poluje na 102
25 wrz 23:52
Lukas:
√8− 2√15+√5 − 2√6 + √8+ 2√2− 2√5− 2√10 = 1
ostatni człon jest dla mnie problemem
25 wrz 23:57
Lukas: Up
26 wrz 17:00
Mila:
czy całe wyrażenie 8+2√2−2√5−2√10 jest pod jednym pierwiastkiem?
Źle widac w mojej przegladarce.
26 wrz 17:44
Mila:
Chyba źle przepisałeś ten przykład.
26 wrz 18:11
MYSZ: 8 + 2√2 − 2√5 − 2√10 = (√5 − √2 − 1)2
26 wrz 18:17
Mila:
Spróbujemy zwinąć wyrażenie pod ostatnim pierwiastkiem
Próba I
(1+√2−√5)2=(1+√2−√5)*(1+√2−√5)=
=1+√2−√5+√2+2−√10−√5−√10+5=
=8+2√2−2√5−2√10 zgadza się
(8+2√2−2√5−2√10 )12=[(1+√2−√5)2]12=(1+√2−√5)
26 wrz 18:17
Lukas:
udowodnij, że zachodzi równość.
√8−2√15+√5−2√6+√8+2√2−2√5−2√10=1
26 wrz 18:19
MYSZ: Teraz moze cos wyjdzie

Pierwsze dwa nawiasy umiesz rozpisac ? ( trzeci juz masz )
26 wrz 18:29
Lukas: tak, napisałem ze 3 człon jest tylko problemem.
26 wrz 18:37
Lukas:
Mila a jest jakiś inny sposób, żeby to zauważyć ?
26 wrz 18:42
Mila:
Na pewno, ale będzie bardziej skomplikowane. Nie przejmuj się tym przykładem, ważne abyś radził
sobie z tymi pierwszymi, gdzie są dwa składniki pod pierwiastkiem.
26 wrz 19:17
Lukas:
Takie umiem zrobić, ale będą na studiach muszę i tak to umieć. A tym bardziej, że teraz matura
R była nietypowa. Policzyłem sobie, że miałbym 50%
26 wrz 19:32
Mila:
No to np tak
√8−2√15=√5−√3
√5−2√6=√3−√2 zwracasz uwagę, aby wynik pierwiastkowania był dodatni
Wtedy mamy:
√5−√3+√3−√2+(8+2√2−2√5−2√10)12=1
√5−√2+(8+2√2−2√5−2√10)12=1+√2
√5+(8+2√2−2√5−2√10)12=1+√2 obie strony są dodatnie /2
5+2*(5*8+5*2√2−5*2√5−5*2√10)12+8+2√2−2√5−2√10=1+2√2+2⇔
2(40+10√2−10√5−10√10)12=2√5+2√10−10 /:2
(40+10√2−10√5−10√10)12=√5+√10−5 obie strony dodatnie /2
(40+10√2−10√5−10√10)=(√5+√10−5 )*(√5+√10−5 )
spróbuj dokończyć, będzie równość prawdziwa, co dowodzi prawdziwości pierwszej równości, bo
przekształcenia są równoważne.
26 wrz 20:14
Lukas:
Dziękuję, to akurat trudniejszy sposób.
26 wrz 20:17
Mila:
Myślę, że nie, więcej liczenia, ale te rachunki powinny być dla Ciebie proste.
Jeśli która linijka nie jest jasna to pytaj.
26 wrz 20:20
Lukas:
5+5√2−5√5+5√2+10−5√10−5√5−5√10+25
40+10√2−10√5−10√10
Dziękuję wyszło prawidłowo.
A co jeśli jedna strona byłaby ujemna ?
26 wrz 20:26
Mila:
Nie możesz wtedy podnosić obu stron do kwadratu, bo może być fałszywy wniosek.
np.
−4<2 /2
16>4 trzeba było zmienic znak, aby otrzymac prawdę.
26 wrz 20:31
Lukas:
Potęgi i pierwiastki mam już przerobione co dalej ?
Zrobiłem prawie wszystkie zadania z zadania.info z tego działu
26 wrz 20:32
Mila:
Dobrze byłoby trochę równań, funkcji.
26 wrz 21:00
Lukas:
Przekształcenia funkcji ? funkcje trygonometryczne ? Równia trygonometryczne ?
26 wrz 21:01
Lukas: ?
26 wrz 21:31
5-latek: Mialem od pewnego czasu pewne podejrzenie . I jednak sie sprawdzilo .
26 wrz 22:23
Lukas:
To miałeś złe podejrzenia...
26 wrz 22:42
Mila:
Tak, Lukas.
26 wrz 23:23
Lukas:
trygonometria jest troszkę trudniejsza. Dziękuję za wskazówkę.
26 wrz 23:37
Mila:
Opanuj dobrze obliczenia procentowe.Na laboratorium będziesz musiał trochę liczyć.
26 wrz 23:43
Lukas:
Tak wiem, chemia i % to nie problem. Mój cel to zaliczyć pierwszy rok i przygotować się do
matury.
26 wrz 23:45
5-latek: Jesli chodzi o trygonometrie to masz to znakomicie wytlumaczone w ksiazce pt. Trygonometria
podrecznik specjalny dla technikow zaocznego szkolenia zawodowego Edward , Jerzy Pokorny
Co prawda wydanie z 1956r i kąty sa podane w stopniach ale to nie problem .
Jesli znajdziesz za nieduze pieniadze na allegro to jak sobie kup
mam jeszce Trygonometria dla klasy X−XI Wieslaw Wojtowicz ,Bronislaw Bielecki , Mieczyslaw
Czyzykowski z 1960r Tez dobra
26 wrz 23:53
 Mimo chęci..
Mimo chęci..


 Tak masz ja narysowac
Tak masz ja narysowac
 Tak to wygląda. Nie jest to wykres dziedziny, tylko wykres f(x) podanej na początku.
Tak to wygląda. Nie jest to wykres dziedziny, tylko wykres f(x) podanej na początku.


 Ja nigdy nie rysowałem wykresu dziedziny, tylko wyznaczałem dziedzinę funkcji
i rysowałem jej wykres (funkcji, nie dziedziny)
Ja nigdy nie rysowałem wykresu dziedziny, tylko wyznaczałem dziedzinę funkcji
i rysowałem jej wykres (funkcji, nie dziedziny)  .
.
 Jeśli dziedzinę, to narysował to bym tak jak wyżej.
Jeśli dziedzinę, to narysował to bym tak jak wyżej.
 up
up
 a nie w układzie wsp x=−3
a nie w układzie wsp x=−3

 Witaj Mila
Witaj Mila 
 Rysunek : 00:26 na osi .
f(x)=√−(x+3)4
D={−3}
f(−3)=√−(−3+3)4=√0=0
x=−3 argument
y=0 wartość funkcji.
Jeśli nie rozumiesz , to zostaw to i idź dalej.
W przypadku:
log2(x2+y)≤1 wyznaczamy dziedzinę
x2+y>0 ( bo liczba logarytmowana jest dodatnia)
y>−x2
W tym przypadku dziedziną jest zbiór punktów których współrzędne(x,y) spełniają warunek y>−x2
,
to znaczy leżących w obszarze nad parabolą y=x2
Rysunek : 00:26 na osi .
f(x)=√−(x+3)4
D={−3}
f(−3)=√−(−3+3)4=√0=0
x=−3 argument
y=0 wartość funkcji.
Jeśli nie rozumiesz , to zostaw to i idź dalej.
W przypadku:
log2(x2+y)≤1 wyznaczamy dziedzinę
x2+y>0 ( bo liczba logarytmowana jest dodatnia)
y>−x2
W tym przypadku dziedziną jest zbiór punktów których współrzędne(x,y) spełniają warunek y>−x2
,
to znaczy leżących w obszarze nad parabolą y=x2







 kisiel jest dobry na stawy , kości i.....
kisiel jest dobry na stawy , kości i..... 
 I..... wiem . Bede go teraz duzo potrzebowal
I..... wiem . Bede go teraz duzo potrzebowal 




 U Pazdry − ponad 61 stron.
U Pazdry − ponad 61 stron.

 z tą trójką
z tą trójką






 Ja poluje na 102
Ja poluje na 102
 Pierwsze dwa nawiasy umiesz rozpisac ? ( trzeci juz masz )
Pierwsze dwa nawiasy umiesz rozpisac ? ( trzeci juz masz )