prosta i okrag dupka: oblicz wzajemne polozenie prostej i okręgu; −3x+y−6=0 (x−1)²+(y+4)²=49

J: Oblicz odległość środka okręgu od prostej i porównaj z promieniem..

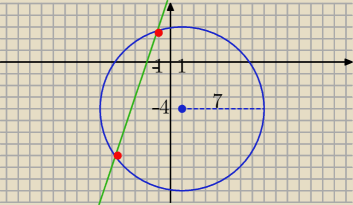
Eta: Położenia okręgu i prostej nie oblicza się tylko określa rysujesz okrąg : S(1,−4) r=7 i prostą y= 3x+6

Eta: A przy okazji zmień nick

PW: Masz już dwa sposoby − obliczenie odległości środka i rysunkowy. Trzeci sposób − "siłowy" − rozwiązać układ równań

	⎧	y = 3x + 6
	⎩	(x−1)2+(y+4)2 = 49

−jeżeli nie ma rozwiązań, to prosta i okrąg nie mają punktów wspólnych. Jeżeli jest jedno rozwiązanie − prosta jest styczna do okręgu. Jeżeli są dwa rozwiązania − prosta przecina okrąg w 2 punktach.

Eta:

MQ: @Eta Skoro gościowi o uroczym nicku dupka odpowiadasz (rozwiązujesz zadanie) Ty, J i PW, to jego nick jest OK. Ja na przykład ludzi, którzy nie trzymają się pewnych zasad (nieprzyzwoite wpisy, nietrzymanie się zasad hierarchii działań, niechlujne wpisy) po prostu nie zauważam.

J: ....podpisuję się pod tym .. .. .szczerze.... nie zwróciłem uwagi na nick

PW: A teraz podam sposób, który tygrysy lubią najbardziej – sposób dla leniwych. Wiadomo, że jeżeli współrzędne punktu P = (x₀,y₀) spełniają nierówność (x₀−1)² + (y₀+4)² < 49, to punkt ten należy do wnętrza rozpatrywanego koła. Niech na przykład P=(−2,0). (−2−1)² + (0+4)² = 25 < 49 − punkt ten należy do wnętrza koła. Jednocześnie jego współrzędne spełniają równanie prostej −3x +y − 6 = 0: −3·(−2) + 0 − 6 =0. Pokazaliśmy w ten sposób, że na prostej istnieje punkt należący do wnętrza koła. Wniosek: prosta i okrąg mają dwa punkty wspólne.

MQ: Drobny kamyczek do ogródka Cienkość metody "dla leniwych" polega na tym, że trzeba wiedzieć (!) jaki punkt wybrać, czyli przynajmniej zrobić sobie rysunek.

PW: Ja to widzę, zawsze zaczynam takie próby od liczb całkowitych. Cienkość metody polega na tym, że mało kto odpowie rzeczowo na pytanie: – A skąd wiadomo, że prosta przechodząca przez punkt wewnętrzny koła ma dwa punkty wspólne z okręgiem?