 Z punktu D należącego od boku AB trójkąta prostokątnego ABC poprowadzono odcinki DE DF w
sposób pokazany na rysunku. Przyprostokątne tego trójkąta mają długości AC = 6 i BC 8 .
Wyznacz długość AD taką aby pole prostokąta CEDF było największe.
Źle mi to wychodziło
Z punktu D należącego od boku AB trójkąta prostokątnego ABC poprowadzono odcinki DE DF w
sposób pokazany na rysunku. Przyprostokątne tego trójkąta mają długości AC = 6 i BC 8 .
Wyznacz długość AD taką aby pole prostokąta CEDF było największe.
Źle mi to wychodziło
| ED | EB | ||
= | |||
| CA | CB |
| x | 8−y | ||
= | |||
| 6 | 8 |
| 0 +8 | ||
p = | = 4 | |
| 2 |
| 24 − 3*4 | ||
y = 4 , x = | = 3 | |
| 4 |
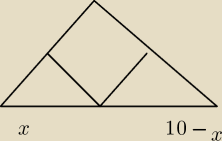 Ta podstawa tak ma wyglądać ?
Ta podstawa tak ma wyglądać ?