wyznacz wartość parametru m, dla których równanie x-|4-2x|=2m ma 2 rozwiązania nadia: witam, mam problem bo ominęła mnie lekcja matematyki i teraz przepisuję zeszyt od koleżanki i nie mogę zrozumieć rozwiązania tego zadania: wyznacz wartość parametru m, dla których równanie x−|4−2x|=2m ma 2 rozwiązania a) dodatnie b) przeciwnych znaków

MQ: To przepisz, co tam koleżanka napisała, to wyjaśnimy.

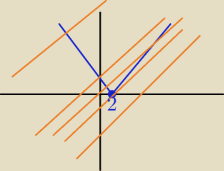
nadia: f(x)= x−2m g(x)= 4−2x y=−2x+4 , x₀=2 − to rozumiem Potem jest jakiś taki układ równań, a niżej: Aby równanie 1 miało 2 rozwiązania dodatnie to f(x) musi spełniać warunek x−2<f(x)<x+4 i właśnie od momentu powstania układu nie rozumiem skąd wzięły się poszczególne funkcje i na jakiej podstawie stawiamy ten warunek

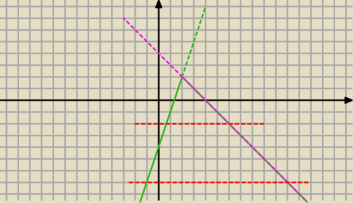
...: "po pierwsze primo" rysujesz wykres funkcji f(x)=x−|4−2x| czyli f(x)=x−|2x−4| rozpatrujesz przedziały: 1^o x∊(−∞, 2) f(x)=x−(−2x+4) f(x)=3x−4 i rysujesz ten wykres w danym przedziale (zielony) 2⁰ x∊<2, ∞) f(x)=x−2x+4 f(x)=−x+4 i rysujesz wykres Ciągłymi masz wykres rozpatrywanej funkcji Dale kroisz ją poziomą y=2m i chyba wszystko jasne −

PW: Funkcja po lewej stronie równania jest określona dwoma różnymi wzorami na dwóch kawałkach osi. Jeden kawałek to te x, dla których 4−2x < 0, drugi − dla których 4−2x ≥ 0. Oba wzory to przepisy na funkcje liniowe, a więc lewa strona ma wykres będący dwiema półprostymi. Po narysowaniu powinno być widoczne, gdzie lewa strona równa jest prawej (gdzie przetną się wykresy – te dwie półprostych z prostą y=2m). Na pewno dobrze przepisane równanie?

PW: A, teraz widzę w czym problem − bardzo sobie na lekcji utrudnili opowiadanie o rozwiązaniu przekształcając równanie. Lepiej w postaci pierwotnej, jak to narysował ... − dwie czerwone poziome kreski to dwie różne wersje y=2m. Ty masz się zastanowić: dla jakich m oba rozwiązania są dodatnie, a dla jakich m jedno dodatnie, a drugie ujemne.

nadia: Kurczę, dziękuję bardzo za próby wyjaśnienia, ale niestety kompletnie nie rozumiem tego zadania W szkole nigdy nie budowaliśmy funkcji z wartością bezwzg. przed którą występuje jakieś działanie, dlatego też przekształciliśmy to.

nadia: czy mogę rozpocząć zadanie od siatki znaków?

Hajtowy: Może podejdź do nauczyciela i powiedz wprost? "Nie było mnie, nie rozumiem! Proszę o indywidualne wytłumaczenie tej lekcji, cześć! "

PW: Spróbuj jeszcze raz przeczytać 19:48 i narysować wykres funkcji po lewej stronie − dojdziesz do rysunku z 19:44 − dwie półproste "tworzące dzióbek" z wierzchołkiem w (2,2). To jest wykres lewej strony. A wykres prawej strony to każda prosta y = 2m.