Zbadaj wklęsłość, wypukłość i punkty przegięcia funkcji: kamczatka: Zbadaj wklęsłość, wypukłość i punkty przegięcia funkcji:

	x3
y =
	x2 − 1

Dziedzina: x² − 1 ≠ 0 x² ≠ 1 x ≠ 1 x ≠ −1

	x2		(x3)'(x2 − 1) − (x2)(x2 − 1)'
y' = (		)' =
	x2 − 1		(x2 − 1)2

	3x2(x2 − 1) − (x2)(2x)
=
	(x2 − 1)2

	3x4 − 3x2 − 2x4		x4 − 3x2
=		=
	(x2 − 1)2		(x2 − 1)2

	x4 − 3x2
y'' = (		)'
	(x2 − 1)2

	(x4 − 3x2)'(x2 − 1)2 − (x4 − 3x2)(x2 − 1)2'
=
	(x2 − 1)4

mnożę przez mianownik bo jest dodatni i : (4x³ − 6x)(x² − 1)² − (x⁴ − 3x²)(2(x² − 1) * (x² − 1)' = (4x³ − 6x)(x² − 1)² − (x⁴ − 3x²)2(x² − 1)*2x = (x² − 1)[(4x³ − 6x)(x² − 1) − (x⁴ − 3x²)4x] mogę coś jeszcze z tym zrobić czy wymnażać?

...: .. tylko po co ?

kamczatka: z tego miejsca zerowe wyznaczać od razu ?

kamczatka: miejsca zerowe powychodzą w pierwiastkach, a ja w odpowiedziach nie mam żadnych pierwiastków, czy coś źle policzyłem ?

...: −do punktów przegięcia wystarczy pierwsza pochodna i analiza co się z nią dzieje przy przejściu przez x_o −do wklęsłości i wypukłości znak drugiej pochodnej (znak a nie wyliczenie które robisz)

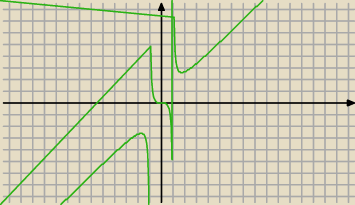
...: f'(x)=0 ⇒ x⁴−3x²=0 ⇒ x²(x²−3)=0 itd

kamczatka: a czemu mi moim sposobem nie wcyhdzi ? bo Twojego nie ogarniam