pomocy kasia 96: Znajdź sumę wszystkich pierwiastków równania |x²−3|x|+3|=1

ICSP: |x² − 3|x| + 3| = 1 |x|² − 3|x| + 3 = 1 |x|² − 3|x| + 2 = 0 |x| = 1 v |x| = 2 x = 1 v x = −1v x = 2 v x = −2 S = 0

PW: To było zadanie dla leniwych. Nie będę liczył pierwiastków. Funkcja po lewej stronie równania jest parzysta: f(−x) = f(x). Jeżeli więc istnieje jakiś pierwiastek x₀, to liczba − x₀ też jest pierwiastkiem − ich suma jest równa 0.

kasia 96: Czyli całą wartość bezwzględną tak jakby opuszczam ?

pigor: ..., np. tak : |x²−3|x|+3|=1 ⇔ x²−3|x|+3= −1 v x²−3|x|+3= 1 ⇔ ⇔ |x|²−3|x|+4= 0 v |x|²−3|x|+2= 0 ⇔ x∊∅ v |x|=1 v |x|=2 ⇔ ⇔ x₁= −1 i x₂= 1 i x₃= −2 v x₄=2 ⇒ x₁+x₂+x₃+x₄= 0 . ...

oskar marcinek: Dziękuje bardzo

pigor: ... , o , PW ; dziękuję, ja też lubię poleniuchować i następnym razem, postaram się o tym pamiętać . ...

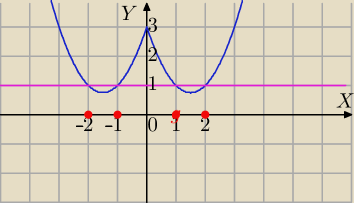
Mila: metoda graficzna. Ilustracja . f(x)=x²−3|x|+3