proszę o sprawdzenie proszę o rozwiązanie: dziękuję Mil iza rozwiązanie ale teraz prosiłbym o sprawdzenie następującego zadania zbadaj liczbę rozwiązań równania w zależności od parametru m , m ∊ R f(x) = 2^Ix−2I+x = m² 1. Ix −2I + x = x − 2+ x =2x −2 dla x−2 ≥0 ⇔ x ≥ 2 i tu szkicuję wykres dla x ≥ 2 funkcja rosnąca 2. Ix −2 I + x = −x+ 2+x = 2 dla x> 2 wtedy f(x) = 2² = 4 funkcja stała f(2) =4 i otrzymujemy m² = 4 ⇒ m = −2 lub m =2 1⁰. równanie nie ma rozwiązania dla m ∊ ( −2 , 2) 2⁰ ma jedno rozwiązanie dla m ∊ ( − ∞,− 2) ∪( 2, + ∞ ) 3⁰ ma nieskończenie wiele rozwiązań dla m ∊ {−2,2} niestety nie narysuję tego tutaj bo nie umiem

PW: Nie wiem dlaczego podstawiasz akurat f(2) =4, gdy wyżej napisałeś, że f jest stała, wszystkie wartości są 4. W 2. powinno być "dla x < 2" W 1. wniosek "funkcja rosnąca" nie jest adekwatny do treści zadania. Powinno być "dla x≥2 funkcja f przyjmuje wszystkie wartości z przedziału (4, +∞)", wnioski dobre.

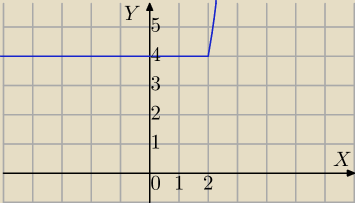
Mila: Pozostaje mi dołączyć wykres, abys sprawdził swój szkic.

PW: Mila, jesteś kochana.

Mila: Pozdrawiam.

proszę o rozwiązanie: słusznie zauważyłaś błąd bardzo dizękuję i za narysowaniu wykresu