Zadania dotyczące ciągów. Proszę o pomoc Mati: Zadania dotyczące ciągów. Zadane z dzisiaj na jutro Każda pomoc mile widziana 1. Wyznacz wszystkie wartości parametru p, dla których nieskończony ciąg (an), gdzie

	pn−2
an =
	(p2+3p)n+1

a) ma granicę równą 3 b) jest rozbieżny do +∞ c) ma granicę równą –2.

	x
2. Rozpatrzmy równanie 1 + f(x) + (f(x))2 + … =		, gdzie lewa strona jest szeregiem
	x−3

geometrycznym zbieżnym, natomiast f(x) jest wartością funkcji f dla argumentu x. Wyznacz wzór i dziedzinę funkcji f oraz narysuj jej wykres. 3. Rozwiąż nierówność: 1 + (x2 – 2x) + (x2 – 2x)2 + … ≤ 1. 4. Udowodnij, powołując się na definicję granicy ciągu liczbowego, że liczba 3 jest granicą ciągu (an), gdzie an = . Następnie ustal, które wyrazy ciągu (an) są oddalone od liczby 3 o mniej niż 0,002.

RM.88: Zadanie 1. W czym problem?

Mati: Jakieś pokichane pn z którym nie wiem co zrobić

PW: Jeżeli nie piszą jakie, to nie "pokichane", ale dowolne rzeczywiste. pn to pewnie "p razy n".

Mati: Fajnie, że masz poczucie humoru, ale ja nie mam w ogóle koncepcji rozwiązania tego zadania

RM.88: Mati oblicz granicę tego ciągu.

Janek191:

	p n − 2		p − 2n
an =		=
	(p2 + 3 p) n + 1		p2 + 3p + 1n

więc

	p − 0		p		1
lim an =		=		=
	p2 + 3 p + 0		p2 + 3 p		p + 3

n→∞

	1
a)		= 3
	p + 3

1 = 3*( p + 3) = 3 p + 9 3 p = − 8

	−8
p =
	3

=========== b) p = − 3 =======

	1
c)		= − 2
	p + 3

1 = − 2*( p + 3) = − 2 p − 6 2 p = − 7 p = − 3,5 ======== Coś mi nie pasuje w b)

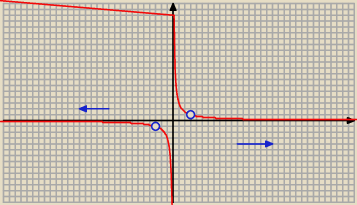
Janek191: z.2

	x
1 + f(x) + ( f(x))2 + .... =
	x − 3

Lewa strona jest równa sumie nieskończonego ciągu geometrycznego : a₁ = 1 q = f(x) , gdzie I f(x) I < 1

	1
SL =
	1 − f(x)

więc mamy równanie

1		x
	=
1 − f(x)		x − 3

x − 3 = x*( 1 − f(x) ) = x − x f(x) x f(x) = 3

	3
f(x) =
	x

========== Ma być

	3
I		I < 1
	x

	3		3
		> − 1 lub		< 1
	x		x

x < − 3 lub x > 3 Df = ( − ∞ ; − 3) ∪ ( 3 ; + ∞ ) =======================

Mati: Oj wielkie dzięki a co to znaczy rozwiązać nierówność?

Janek191: z.3 1 + ( x² − 2x) + ( x² − 2x)² + ... ≤ 1 Lewa strona nierówności jest sumą nieskończonego ciągu geometrycznego : a₁ = 1 q = x² − 2x , gdzie I x² − 2 x I < 1

	a1		1		1
SL =		=		=
	1 − q		1 − ( x2 − 2x)		1 + 2 x − x2

Mamy zatem nierówność

1
	≤ 1
1 + 2x − x2

to 1 + 2 x − x² ≥ 1 2 x − x² ≥ 0 x*( 2 − x) ≥ 0 x₁ = 0 x₂ = 2 a = − 1 < 0 − ramiona paraboli o równaniu y = − x² + 2 x skierowane są do dołu , zatem x ∊ < 0 ; 2 > −−−−−−−−− ale I q I < 1 więc I x² − 2 x I < 1 x² − 2 x > − 1 lub x² − 2 x < 1 x² − 2 x + 1 > 0 lub x² − 2 x − 1 < 0 1) x² − 2x + 1 > 0 ( x − 1)² > 0 dla x ≠ 1 2) x² − 2 x − 1 < 0 Δ = (−2)² − 4*1*(−1) = 4 + 4 = 4*2 √Δ = 2√2

	2 − 2√2
x3 =		= 1 − √2
	2

	2 + 2√2
x4 =		= 1 + √2
	2

x ∊ ( 1 − √2 ; 1 + √2) ( 0 ; 2) ∩ ( 1 − √2 ; 1 + √2 ) \ { 1 } = ( 0 ; 1) ∪ ( 1 ; 2) Odp. x ∊ ( 0 ; 1) ∪ ( 1 ; 2) =====================

Janek191: z.4 Treść zadania nie jest kompletna, więc nie da się go rozwiązać

Sławek: Jeśli chodzi o zadania 1 b) to gdy p=−3 to: a_n =⁻³ⁿ⁻²_(9−3)n+1 = ⁻³ⁿ⁻²₁=−3n−2 → − 3* ∞−2 = −∞ (przy n→∞) Stąd uważam, że nie istnieje takie p, dla którego ciąg dąży do +∞